Does the real resonance structure have a lower or higher total potential energy than each of the contributing structures?
1 Answer
Neither; it is just more spread out, and thus entropically favored.
Assuming you mean the resonance hybrid structure relative to the possible resonance structures, let's see...
Consider
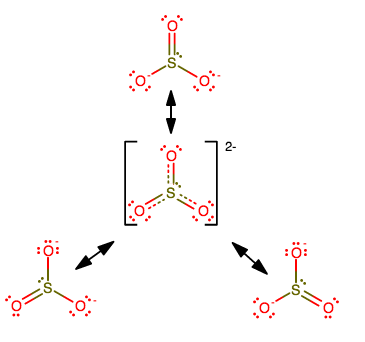
The central structure is the resonance hybrid structure that consists of contributions from all three resonance structures.
Now, let's consider how the energy might change.
- The atoms are the same atoms. No atom's identity changed.
- For this molecule, the skeletal structure is the same skeletal structure. The molecule didn't change atom positions.
- The electrons have moved.
So, the only way the energy could change is based on where the electrons have moved.
HOW HAVE THE ELECTRONS "MOVED"?
Since the charge remained the same but the type of bonds changed, the only thing that happened to the electrons going from the resonance structure to the resonance hybrid structure is that they redistributed to form more "evened-out" bonds.
In other words, the double bond became a "less-than-double" bond.
A "LESS-THAN-DOUBLE" BOND
Now, let's figure out what the "less-than-double" bond really means.
In any chosen resonance structure for
That's not literally possible. But consider that the bond order is:
#"BO" = 1/2("Bonding e"^(-) - "Antibonding e"^(-))#
The bond order of a sigma bond is
The proper way to describe this "less-than-double" bond containing
#"BO" = stackrel("1 sigma")overbrace(1) + stackrel("2/3 pi")overbrace("1/3") = \mathbf("4/3")# .
Thus, we should say that the resonance hybrid structure of
Just so we know we have it right...
Note that:
- One double bond (bond order:
#2# in this case) plus two single bonds (bond order:#1# each in this case) gives a total bond order of#4# . - Three identical
#"4/3"# bonds added together gives a total bond order of#4# as well.
So we didn't lose any electrons.
CONCLUSIONS
Now that we know how the electron density is distributed, we've accounted for where the electrons have gone.
Recall that the amount of energy is supposed to always be conserved. From accounting for where the electrons have gone, we can conclude that the energy has not been lost from the molecule to stabilize it---it has been redistributed.
Therefore, the resonance hybrid structure of
(In other words, more parts of the molecule are happy, thereby making the whole molecule happier.)
You can read this if you don't understand why we chose to distribute the electrons evenly in

