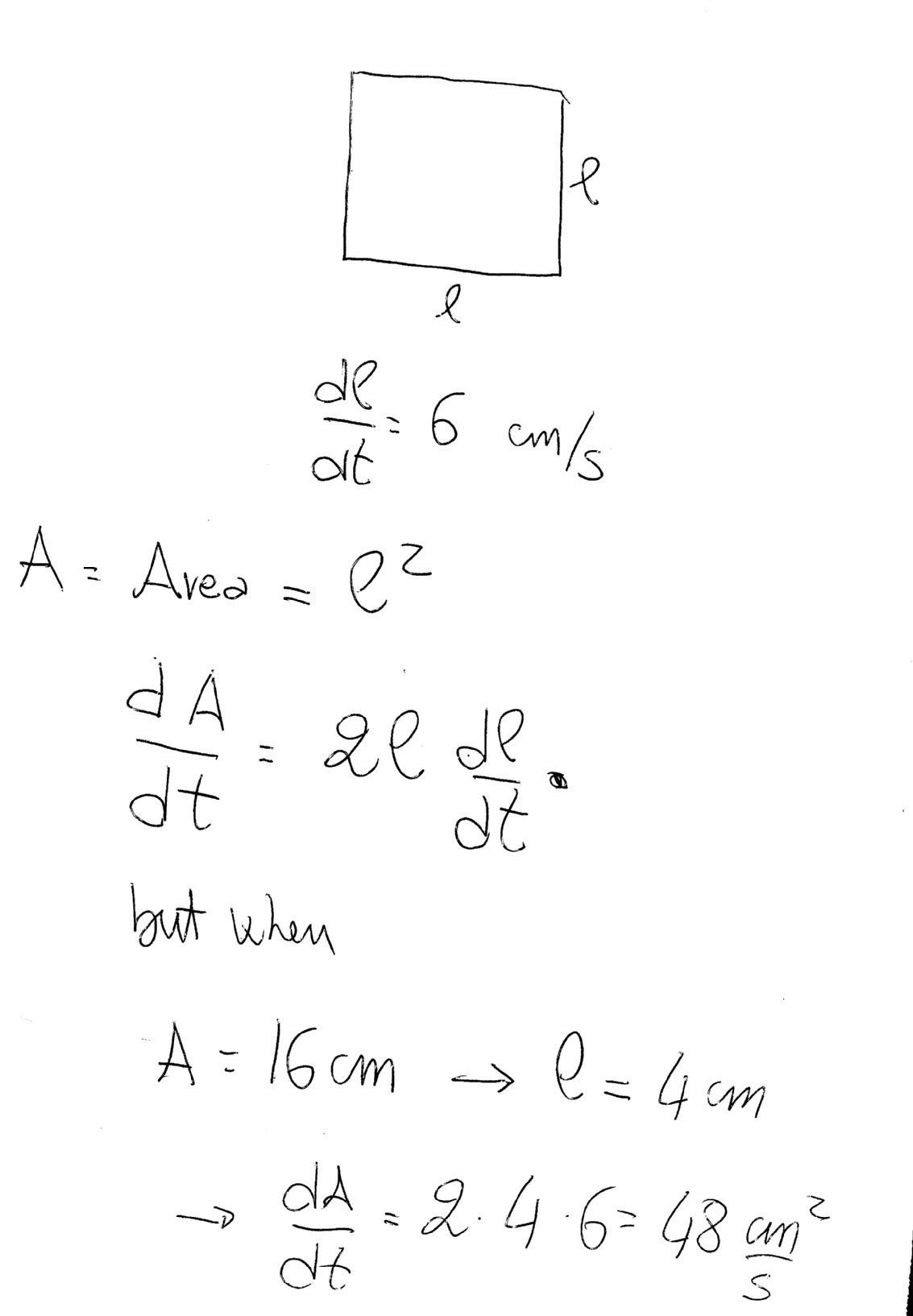
Each side of a square is increasing at a rate of 6 cm/s. At what rate is the area of the square increasing when the area of the square is 16 cm^2?

Question

139275 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2015-04-06T18:48:58

Consider the side of the square as a function of time #l(t)# so:
enter image source here

Answer 2 · 2015-04-06T18:57:29

The Area, A is increasing by #48 # #cm^2s^-1#

Area, A = #s^2#
#s# is the side length

#=> (dA)/(dt)= 2s*(ds)/(dt) ## " {[Chain rule](http://socratic.org/calculus/basic-differentiation-rules/chain-rule)}"#

#(ds)/(dt) = 6 " cm/s"#

When A = 16 # cm^2 => 16 = s^2#

#=> s = sqrt(16) => s = 4 cm#

Hence,

#=> (dA)/(dt) = 2xx4xx6 = 48 cm^2s^-1#