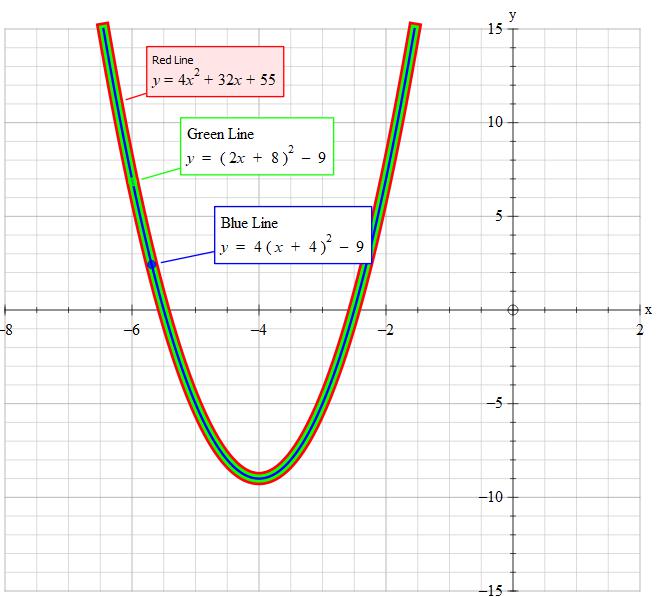
Express #4x^2+32x+55# in the form #(ax+b)^2+c#, where a, b and c are constants and a is positive?
3 Answers
Explanation:
Here,
Changing
we have
We have,
Since
and
changing now,
Is the question correct? The normal format for this question type is completing the square
Answering for
Explanation:
You can change any equation you wish into the format you wish as long as you add to it a correction that if applied with transform it back again.
A bit like
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Given
then determine the value of
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
I was challenged once on a point so I am doing it this way:
For each change we must include a correction. The value of this correction will be different as we proceed step-wise through the modifications on the path to the final format.
At this point
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Factor out the 4
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Set
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
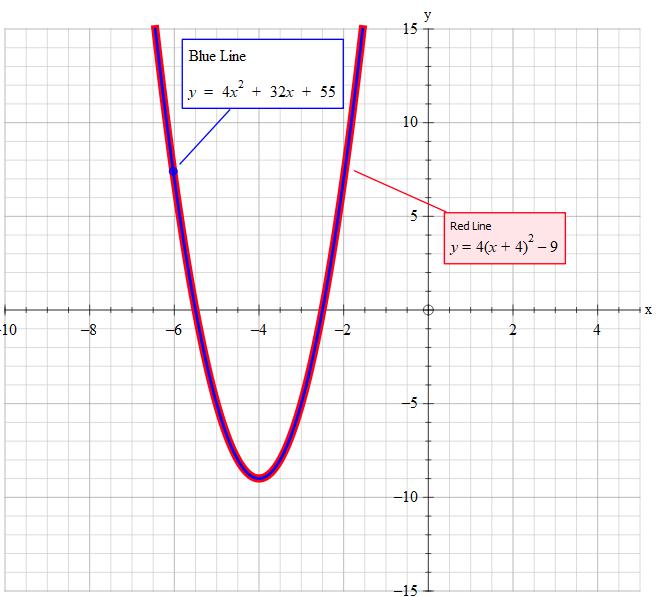
Assuming your question is correct.
'Forcing' the completed square solution in my other answer into this format we have:
Explanation:
Expanding :