Let #(r,theta)# be the Polar coordinates of #z_2#. We have to find some sort of relations between the Polar coordinates and the Cartesian ones, which we know are #(4,4)#.
Let #zeta=x+yi# be a complex number with polar coordinates #(r,theta)#. We can represent it is:
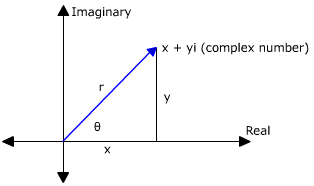
From the diagram above, we can deduce the following properties:
#{(r^2=x^2+y^2),(x=rcostheta),(y=rsintheta):}#
Let us return to our particular case, #z_2 = 4+4i#. Instead of brute-forcing it through the formulae, we can instead factor out the #4#:
#z_2 = 4(color(red)(1+i))#
Now, in the complex plane, we know that #1# and #i# have the same magnitude, thus, the complex number #1+i# forms a isosceles right triangle, with angle #theta=pi"/"4#.
Since both #"Re"(z_2)# and #"Im"(z_2)# are positive, our #theta# must be #pi"/"4#.
We know that for this type of triangle, the hypotenuse is the lenght of its side times #sqrt2#. The lenght of each of the legs in our triangle #4#, as we have #"Re"(z_2)="Im"(z_2)=4#.
#=> r=4sqrt2#
Thus, the Polar coordinates of #z_2# are #(4sqrt2,pi/4)#.
In other words, #z_2 = 4sqrt2e^(ipi/4)#, by Euler's identity.


