Polar Coordinates
Key Questions
-
Answer:
I am assuming that you want to convert a point in Cartesian Coordinate form to Polar Coordinate Form.
I will use an example in the explanation below.
Explanation:
Let us say that we want to convert a point
#(0, 2)# in Cartesian Form to Polar Form.Let us analyze the image below:
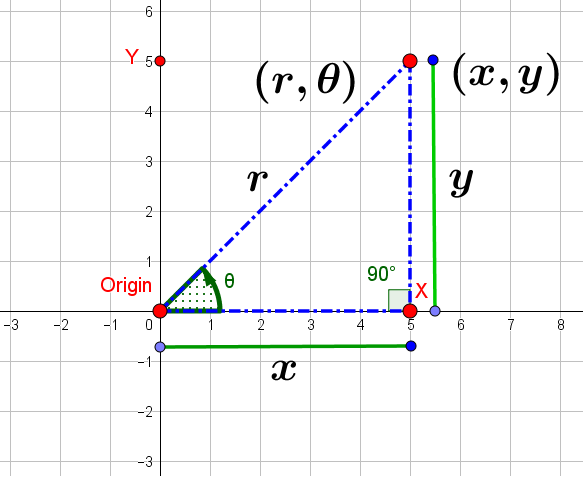
We have a right-triangle and hence we can use Pythagoras Theorem to define a relationship:
#x^2 + y^2 = r^2# #tan theta = y/x# We can see that
#cos theta = x/r# Hence,
#color(blue)(x=r cos theta# #color(red)([ 1 ]# #sin theta = y/r# Hence,
#color(blue)(y = r sin theta# #color(red)([ 2 ]# Observe that, if we are given the point
#(x, y)# , then we can define#(r, theta)# and express#(x,y)# in terms of#(r cos theta, r sin theta)# .Now, let us work on the point in Cartesian coordinate form, in our example:
#(0,2)# Let us plot this point and look at the graph:
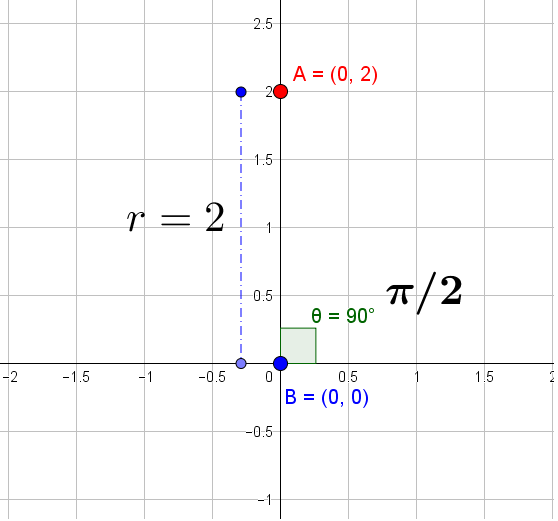
Now, we are in a position to convert the
#(0, 2)# to equivalent Polar form using#color(red)([ 1 ]# and#color(red)([ 2 ]# Polar form is
#color(green)((r, theta)# #rArr color(blue)((2, pi/2)# Hope it helps.
-
Yes! It is possible to derive formulae for both the two-dimensional and three-dimensional cases in polar coordinates. The following are the formulae:
2-D Polar Coordinates :
#\vec{r_A}=(r_A,\theta_A); \qquad \vec{r}_B=(r_B, \theta_B)#
#S=\sqrt{|\vec{r}_B-\vec{r}_A|^2} = \sqrt{r_A^2+r_B^2-2r_Ar_B\cos(\theta_B-\theta_A)}# 3-D Spherical Polar Coordinates :
#\vec{r_A}=(r_A,\theta_A,\phi_A); \qquad \vec{r}_B=(r_B, \theta_B, \phi_B)#
#S=\sqrt{|\vec{r}_B-\vec{r}_A|^2}#
#= \sqrt{r_A^2+r_B^2-2r_Ar_B[\sin\theta_A\sin\theta_B\cos(\phi_B-\phi_A)+\cos\theta_A\cos\theta_B]}# Deriving these formulae requires writing the position vectors in their cartesian forms and apply the Pythagorous Theorem to find the distance between two points in space. The following trigonometric identities might be useful for this problem :
#\cos(A-B)=\cos(A)\cos(B)+\sin(A)\sin(B)# #\sin^2A+\cos^2A=1#
Derivation of 2-D Formula :
#\vec{r}_A=(r_A, \theta_A) = (X_A, Y_A); \qquad \vec{r}_B=(r_B, \theta_B) = (X_B, Y_B);#
#X_A=r_A\cos\theta_A, \quad Y_A=r_A\sin\theta_A; #
#X_B=r_B\cos\theta_B, \quad Y_B=r_B\sin\theta_B; # The distance between the two points is:
#S=\sqrt{|\vec{r}_B-\vec{r}_A|^2} = \sqrt{(X_B-X_A)^2+(Y_B-Y_A)^2}#
#S=\sqrt{(r_B\cos\theta_B-r_A\cos\theta_A)^2+(r_B\sin\theta_B-r_A\sin\theta_A)^2}# Upon expanding the squares and further simplification,
#S=\sqrt{r_A^2(\cos^2\theta_A+\sin^2\theta_A)+r_B^2(\cos^2\theta_B+\sin^2\theta_B)-2r_Ar_B(\cos\theta_A\cos\theta_B+\sin\theta_A\sin\theta_B)}#
#S=\sqrt{r_A^2+r_B^2-2r_Ar_B\cos(\theta_B-\theta_A)}# Derivation of 3-D Formula :
#\vec{r}_A=(r_A, \theta_A,\phi_A) = (X_A, Y_A,Z_A); #
#\vec{r}_B=(r_B, \theta_B,\phi_B) = (X_B, Y_B,Z_B);# #X_A=r_A\sin\theta_A\cos\phi_A, \quad Y_A=r_A\sin\theta_A\sin\phi_A; Z_A=r_A\cos\theta_A# #X_B=r_B\sin\theta_B\cos\phi_B, \quad Y_B=r_B\sin\theta_B\sin\phi_B; Z_B=r_B\cos\theta_B# The distance between the two points is:
#S=\sqrt{|\vec{r}_B-\vec{r}_A|^2} = \sqrt{(X_B-X_A)^2+(Y_B-Y_A)^2+(Z_B-Z_A)^2}# #(X_B-X_A)^2 =(r_B\sin\theta_B\cos\phi_B-r_A\sin\theta_A\cos\phi_A)^2# #(Y_B-Y_A)^2 =(r_B\sin\theta_B\sin\phi_B-r_A\sin\theta_A\sin\phi_A)^2# #(Z_B-Z_A)^2=(r_B\cos\theta_B-r_A\cos\theta_A)^2#
Upon expanding the squares and further simplification,
#S=\sqrt{r_A^2(\cos^2\theta_A+\sin^2\theta_A)+r_B^2(\cos^2\theta_B+\sin^2\theta_B)-2r_Ar_B[\sin\theta_A\sin\theta_B (\cos\phi_A\cos\phi_B+\sin\phi_A\sin\phi_B)+\cos\theta_A\cos\theta_B]}# #=\sqrt{r_A^2+r_B^2-2r_Ar_B[\sin\theta_A\sin\theta_B \cos(\phi_B-\phi_A)+\cos\theta_A\cos\theta_B]}# -
One of the most interesting differences is that every point in the plane has exactly one representation as a pair of coordinates in the rectangular (or any other parallelogram) coordinate system, but has infinitely many representations in polar coordinates.
Example:
The point whose rectangular coordinates are
#(1,1)# corresponds to polar coordinates:
#(sqrt2, pi/4)# and also#(sqrt2, (9 pi)/4)# and#(sqrt2, (-7 pi)/4)# and#(-sqrt2, ( 5 pi)/4)# and infinitely many others. -
A polar coordinate system consists of a polar axis, or a "pole", and an angle, typically
#theta# . In a polar coordinate system, you go a certain distance#r# horizontally from the origin on the polar axis, and then shift that#r# an angle#theta# counterclockwise from that axis.This might be difficult to visualize based on words, so here is a picture (with O being the origin):

This is a more detailed picture, depicting a whole polar coordinate plane (with the
#theta# 's in radians):
The origin is in the middle, and each circle represents a different
#r# (which is actually a radius). If you follow the line of that given circle with radius#r# along the angle, you can get polar coordinate points in the form#(r,theta)# Note that polar coordinates/equations have Cartesian equivalents shown below:

-
Explanation:
I can give a simple answer, i.e. a combination of a radial coordinate r and the angle
#theta# , which we give as an ordered pair#(r,theta)# .I believe, though, that reading up what is said other places on the Internet, for instance http://mathworld.wolfram.com/PolarCoordinates.html, will be of more help.