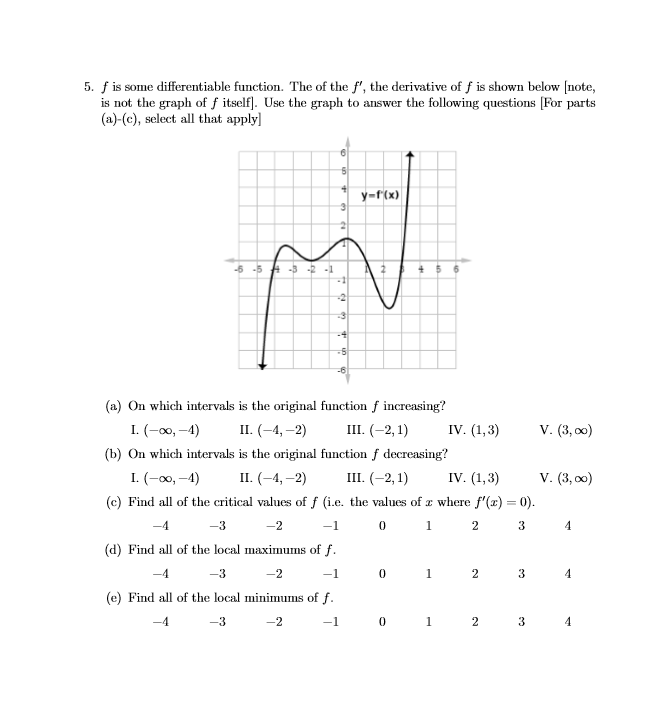
a. #f# increases wherever #f'>0#. Examining the graph, we see #f'>0# on #(-4, 2), (-2,1) (3, oo).# So, the answer is II., III., V.
b. #f# decreases wherever #f'<0#. This holds true for #(-oo, -4), (1, 3).# So, the answer is I., IV.
c. #f'=0# (crosses or touches the #x-#axis) at #x=-4, -2, 1, 3#.
d. A local maximum requires #f'# to change from positive to negative, I.E., #f# to go from increasing to decreasing. #f'# goes from positive to negative at #x=1.#
e. A local minimum requires #f'# to change from negative to positive, I.E., #f# to go from decreasing to increasing. This happens at #x=-4, x=3#
So, we see although #x=2# is a critical value, it is neither a positive or negative. This does happen on occasion; not every critical value is an extreme value.