Question

F(x)=x+2 g(x)=x^2+4 Whats the function and relation?

Answer 1

`" "`
Please read the explanation.

Explanation:

`" "`
Definition of a Relation:

A Relation can be defined as a set of elements - both input and output values - available as ordered pairs.

There are no special rules.

Definition of a Function:

A Function can be defined as a set of ordered pairs in which each element of `color(red)(x` has one and only one element of `color(red)(y` associated with it.

However, it is interesting to note that two elements of `color(red)(x` may have same element of `color(red)(y` associated with them.

We are given two relations:

`color(red)(f(x)=x+2`

`color(red)(g(x)=x^2+4`

Please note that the first relation

`color(red)(f(x)=x+2`

is linear

while

the second relation

`color(red)(g(x)=x^2+4`

is quadratic

`color(blue)("What do we need to do ?"`

We need to determine whether any of these relations is a function.

We can set up the relations as tables of ordered pairs:

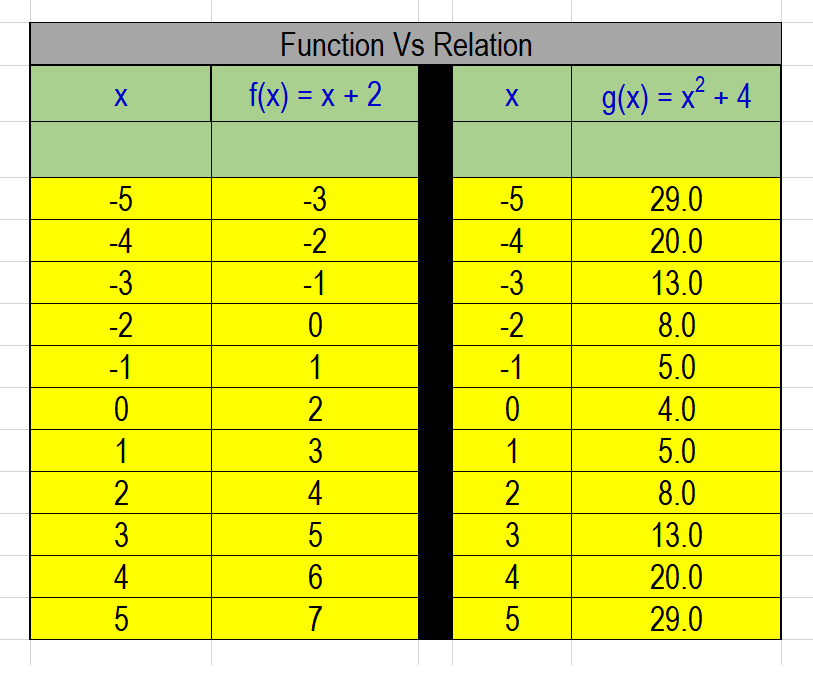
The relation `color(red)(y=f(x)=x+2` has a unique `color(red)(y` value for the corresponding element of `color(red)(x` for the ordered pairs.

Hence, this relation represents a function.

The relation

`color(red)(y=g(x)=x^2+4`

has the same `color(red)(y` value for two distinct elements of `color(red)(x`.

Hence, ordered pairs `color(red)((x,y)` are not one-to-one relationships.

It is still a function.

We can easily observe these points using their graphs:

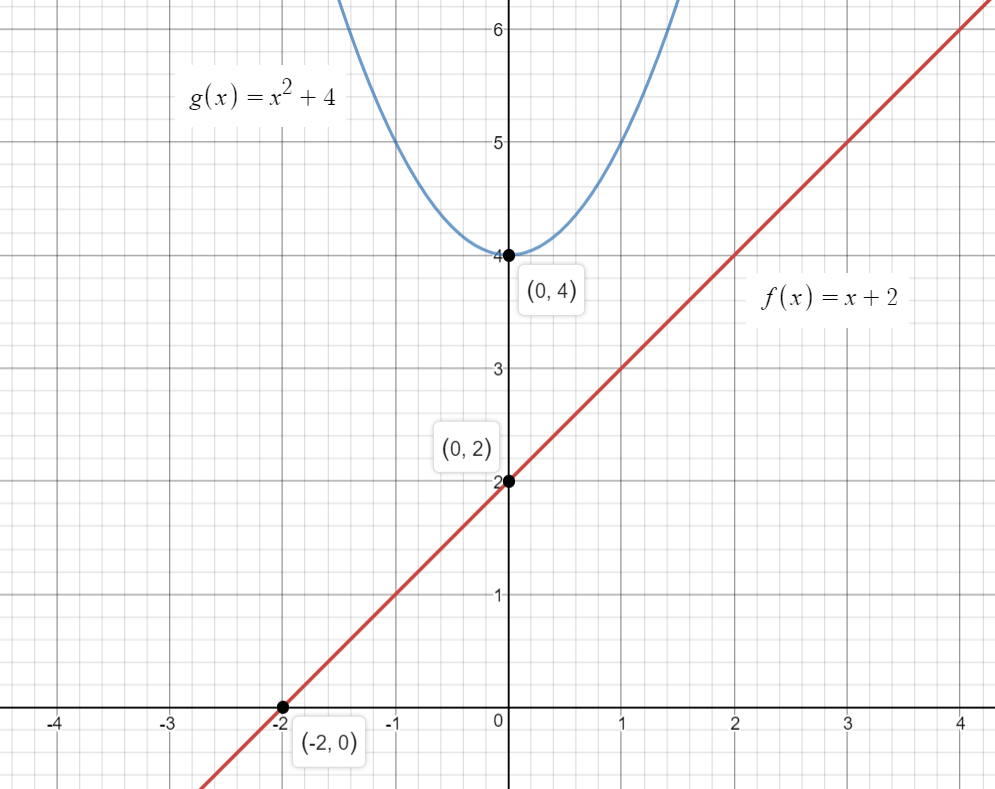
There is an alternative method as well:

We can perform the vertical line test for the graphs:

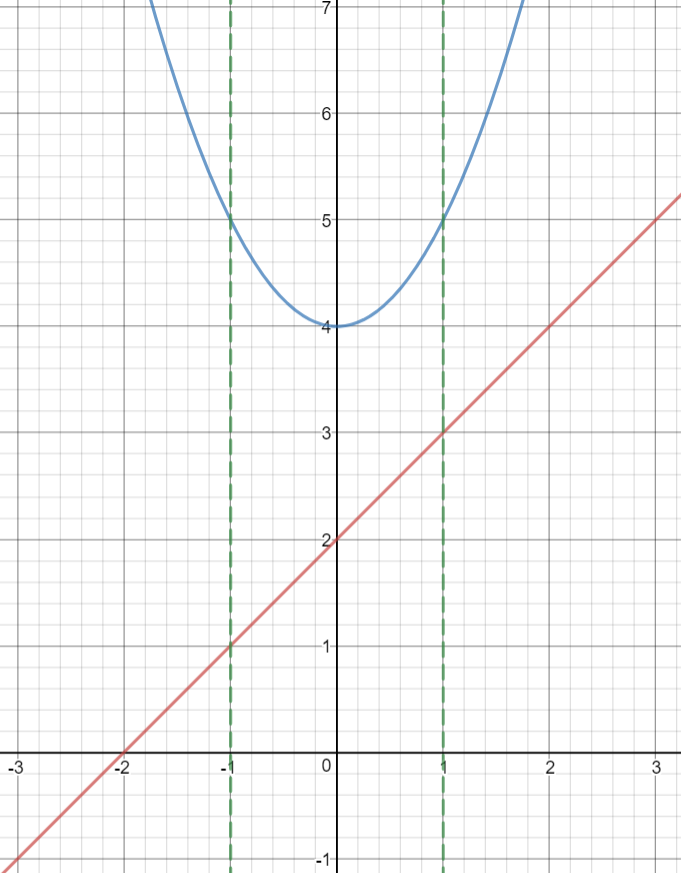
Vertical Lines intersect the graphs exactly at one point.

Hence, the relations pass the vertical line test and we conclude that both the given relations are function.