Vertical Line Test
Key Questions
-
The vertical line test is used to find out if a relation is a function.
If a vertical line is drawn for each value in the domain of a relation and if that line only intersects the relation once then the relation is a function.
#y=3x+4# is a line and passes the vertical line test, it is a function.#y=x^2# is a parabola and passes the vertical line test, it is a function.#x^2+y^2=1# is a circle and fails the vertical line test, it is not a function. -
Answer:
#" "#
Please read the explanation.Explanation:
#" "#
Let us say we have a graph drawn for a mathematical relation.#color(red)(y=f(x)=x^2# This is a mathematical relation, as for every value of
#color(blue)(x# , there is a corresponding value of#color(blue)(y# .To check whether this graph is a function, a Vertical Line Test can be used.
Let us examine the following graph drawn for the mathematical relation:
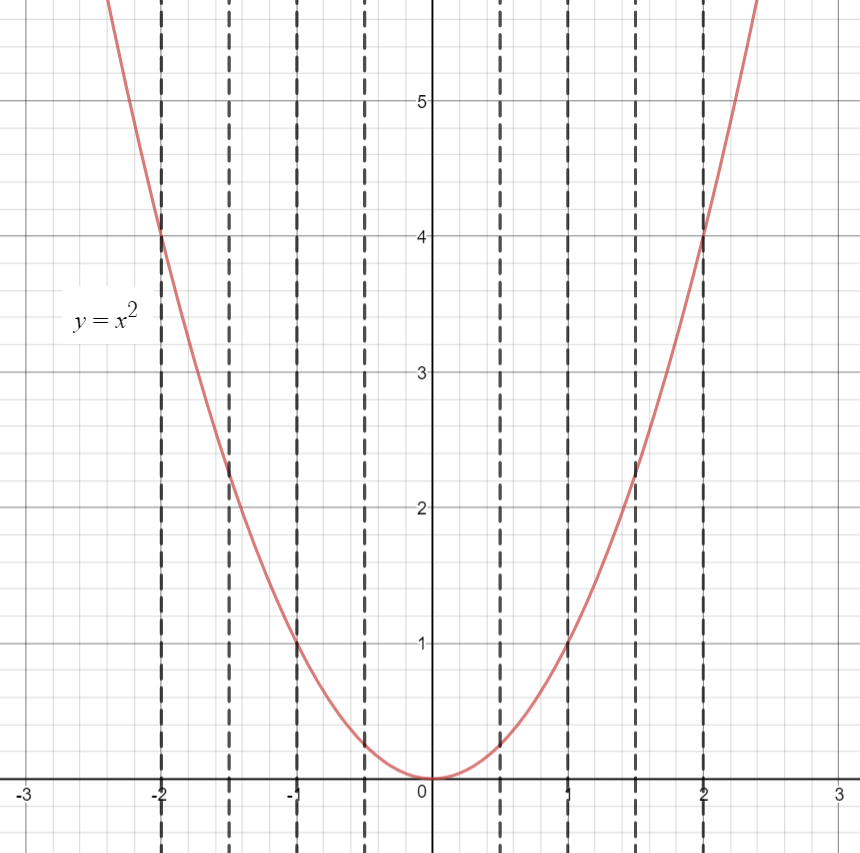
Can you observe the vertical lines drawn for various values of
#color(red)(x# ?All of these vertical lines intersect the graph at one point only.
If there is just one point of intersection,
that would mean,
for every x-value, there is just one unique y-value.
This property proves that the given mathematical relation
#color(red)(y=f(x)=x^2# is a mathematical function.
Hence, the vertical line test works in determining whether a given relation is a function.
Let us try one more mathematical relation:
#color(blue)(y^2=-4x# This mathematical relation creates a parabola and the parabola is symmetric about the x-axis, at
#color(red)(y=0# .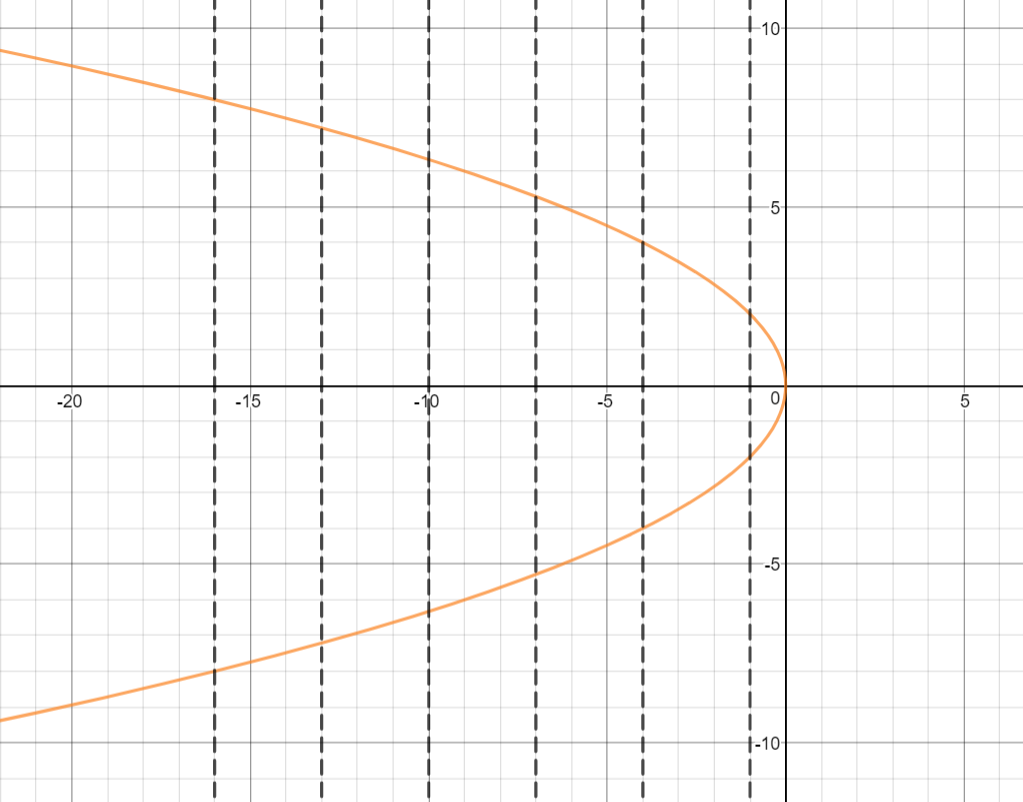
This mathematical relation
#color(blue)(y^2=(-4x)# is NOT a function,as the vertical line test fails.
Hope it helps.
-
Given two sets
#A# and#B# (they could be sets of numbers, but also what you want...), a relation is a certain number of arrows that joints some elements of#A# with some elements of#B# .A function is a particular relation that joints every element of
#A# with one and only one element of#B# . -
Answer:
The vertical line test is a test that can be performed on a graph to determine if a relation is a function.
Explanation:
The vertical line test is a test that can be performed on a graph to determine if a relation is a function. Recall that a function can only be a function if every value of x maps to only one value of y, that is to say it's a one-to-one function or a many-to-one function.
If every value of x only has one value of y, any vertical line drawn on the graph should only intersect the graph of the function once. If this is true for any point on the graph it is said to be a function.
If you take a look at this graph you can see that any vertical line drawn will intersect the graph only once. (However horizontal lines may intersect the graph more than once)
graph{x^2 [-10, 10, -5, 5]}
An example of a relation that is not a function is
#x^2 +y^2=1# Note that this is not a function since vertical lines can be drawn that intersect the relation more than once. It is said to be a one-to-many relation or in this case actually a many-to-many relation.
graph{x^2 +y^2=1 [-10, 10, -5, 5]}
Questions
Expressions, Equations, and Functions
-
Variable Expressions
-
Expressions with One or More Variables
-
PEMDAS
-
Algebra Expressions with Fraction Bars
-
Patterns and Expressions
-
Words that Describe Patterns
-
Equations that Describe Patterns
-
Inequalities that Describe Patterns
-
Function Notation
-
Domain and Range of a Function
-
Functions that Describe Situations
-
Functions on a Cartesian Plane
-
Vertical Line Test
-
Problem-Solving Models
-
Trends in Data