Find a general solution y (x) of non-homogeneous linear equations of the 2nd order with constant coefficients and special right side. How to solve? (pictures below) Thank you a lot!
here:
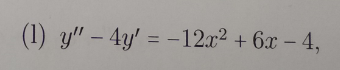
this should be solution
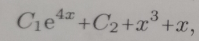
here:
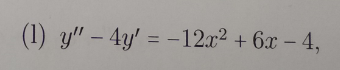
this should be solution
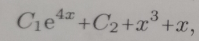
1 Answer
Solve the differential equation:
This is a non-homogeneous linear equation with constant coefficients, so we start by solving the characteristic equation of the corresponding homogeneous equation:
So the general solution of the homogeneous equation is:
In the complete equation, the known term is in the form
As
where
Then:
and equating the coefficients of the same degree in
So:
and the complete solution is:

