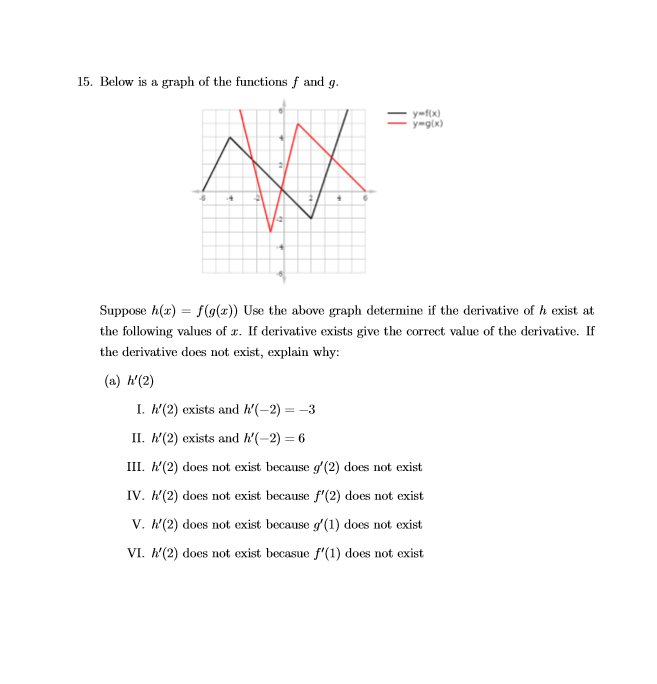
Find #h'(2)#? (see image below)
1 Answer
Mar 14, 2017
The graphs above were:
Some things to keep in mind:
- Note that
#h(x) = f(g(x))# . This means you will have to find a value for#g(x)# , and use that value for the argument of#f(x)# . For instance, for some#g(3) = w# , we have that#h(3) = f(g(3)) = f(w)# . - We should recognize that the derivative at a corner, e.g. when the graph abruptly changes slope, is undefined.
#h'(x) = f'(g(x))*g'(x)# by the chain rule.
Thus,
Reading from the above graph:
For
#h'(2) = f'(g(2))g'(2)#
#= f'(4)g'(2)#
#= 3*-1#
#= -3#
Therefore,
#h'(-2) = f'(g(-2))g'(-2)#
#= f'(1)g'(-2)#
#= -1*-4#
#= 4#
Well, we found that

