Find the area of an equilateral triangle with apothem 7 cm? Round to the nearest whole number.
help me.
help me.
1 Answer
I got
Explanation:
The apothem of the triangle will also be the triangle's height.
Let's work out the height of an equilateral triangle in terms of its sides.
Say we have an equilateral triangle of side
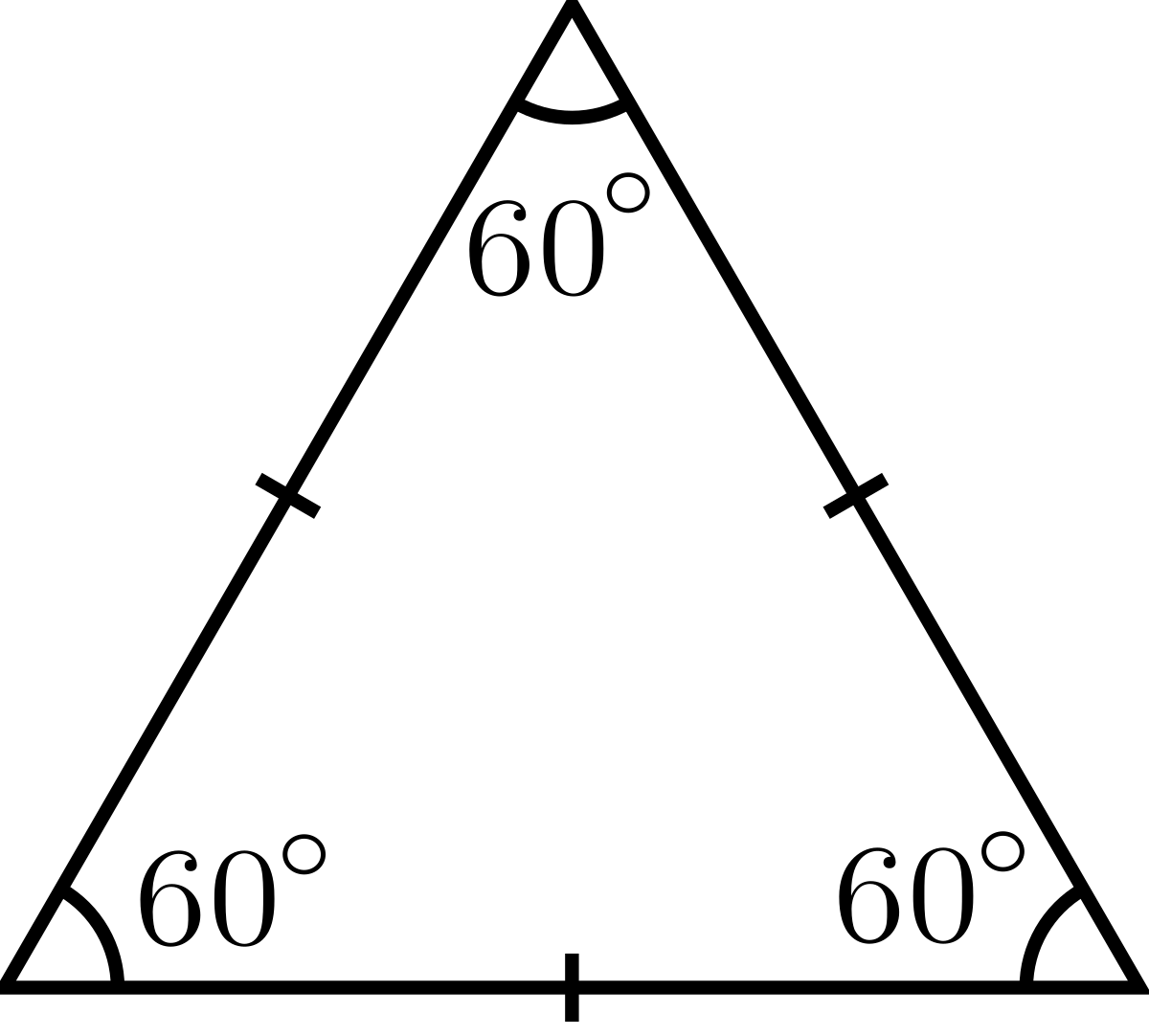
Its height will be the perpendicular bisector of another side, let's call it
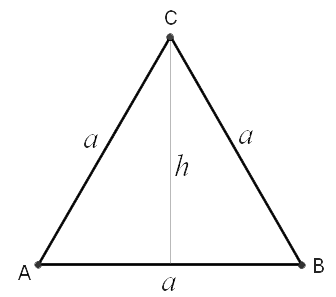
As you can see here, we split the triangle into
Now, let's work out the height
We can use Pythagoras's theorem to work out the height,
We got:
So, the height of an equilateral triangle with sides
Now, we can put this formula back into our original problem.
We have the apothem or the triangle's height as
So, the triangle's side will be
The area of a triangle is given by
Plugging in our values, we get

