Find the area of the shaded region (green) knowing the side of square is #s = 25 cm#?
2 Answers
I don't think there is enough information to find the area of all the shaded region, since we have really no information about the dimensions of the circle. Therefore, I think what they want you to find is the area of the half square.
Explanation:
Use the formula for area of a triangle:
Therefore, the area of the shaded half square is 312.5 square centimetres.
I could be wrong about it being impossible to find the area of the complete shaded area. I have flagged my answer so that other contributors can think about it.
Hopefully this helps.
Explanation:
The area of the green space can be calculated as the difference between the area of the square and the area of the semicircle. The area of the square is easy to calculate as we are given the side length, and we know the area of the semicircle is half the area of the circle with the same radius. Then, to solve the problem, the main task is to find
The picture seems to indicate that the diagonal of the square is tangent to the semicircle. We will operate based on that assumption.
We can label the picture as follows:
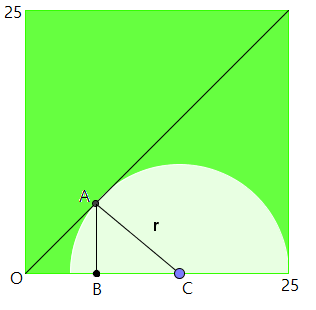
Imposing the image on a coordinate plane with the lower left corner of the square at
Because the diagonal is tangent to the circle and
Then, by symmetry,
As the sum of those line segments together with a radius of the semicircle gives us the base of the square, we have
Next, noting that
Applying the quadratic formula, we get
As we know
Now, given the area of the square as


