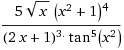Steps in Logarithmic Differentiation
1. Take natural logarithms of both sides of an equation y=f(x) and use the Laws of Logarithms to simplify.
2. Differentiate implicitly with respect to x
3. Solve the resulting equation for y’
4. Replace y with original equation
Let #y=(5sqrtx (x^2+1)^4)/((2x+1)^3tan^5(x^2))# and lets rewrite the equation as #y=(5x^(1/2)(x^2+1)^4)/((2x+1)^3tan^5(x^2))#
Now use the following Properties of Logarithms to expand the original problem
#color(red)(log_b(xy)=log_b x+log_b y#
#color(red)(log_b(x/y)=log_b x-log_b y#
#color(red)(log_bx^n=n log_b x#
That is,
#color(blue)(ln y=ln((5x^(1/2)(x^2+1)^4)/((2x+1)^3tan^5(x^2)))#
#color(blue)(ln y =5ln x^(1/2)+ln(x^2+1)^4-ln(2x+1)^3-ln (tan x^2)^5#
#color(blue)(ln y =5/2 ln x+4 ln(x^2+1)-3ln(2x+1)-5 ln(tan x^2)#
#color(blue)(d/dx (ln y =5/2 ln x+4 ln(x^2+1)-3ln(2x+1)-5 ln(tan x^2))#
#color(blue)(1/y dy/dx = 5/2 1/x + 4 ((2x)/(x^2+1))-3(2/(2x+1))-5((2xsec^2(x^2))/tan x^2)#
#color(blue)(1/y dy/dx = 5/(10x)+(8x)/(x^2+1)-6/(2x+1)-(10xsec^2(x^2))/tan x^2)#
#color(blue)( dy/dx = [5/(10x)+(8x)/(x^2+1)-6/(2x+1)-(10xsec^2(x^2))/tan x^2]*y#
#color(blue)( dy/dx = [5/(10x)+(8x)/(x^2+1)-6/(2x+1)-(10xsec^2(x^2))/tan x^2]*[(5sqrtx (x^2+1)^4)/((2x+1)^3tan^5(x^2))]#