Find the derivative of the function?
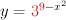
1 Answer
Mar 7, 2017
Explanation:
Given:
Use the natural logarithm on both sides:
Use the property
Differentiate both sides:
Multiply both sides by y:
Substitute
