Question

Find the dimension of the rectangle of greatest area that can be inscribed in a circle of radius r?

Answer 1

The rectangle will be a square of side length `1/sqrt(2)r`

Explanation:

Let's draw a diagram:

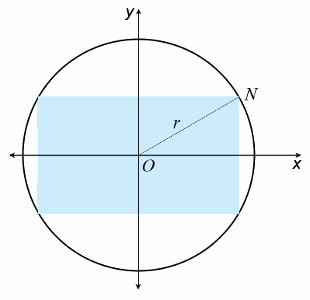
As you can see from the diagram, by pythagoras, `x^2 + y^2 = r^2`, or `y^2 = r^2 - x^2 -> y = sqrt(r^2 - x^2)`

The area will be `A = 2x(2y) = 2x(2sqrt(r^2 - x^2)) = 4xsqrt(r^2 - x^2)`

If we take the derivative of this with respect to `x` we get

`A' = 4sqrt(r^2- x^2) + (4x(-2x))/(2sqrt(r^2 - x^2))`

`A' = 4sqrt(r^2 - x^2) - (8x^2)/(2sqrt(r^2 -x^2))`

`A' = 4sqrt(r^2 - x^2) - (4x^2)/sqrt(r^2 - x^2)`

`A' = (4(r^2 - x^2) - 4x^2)/sqrt(r^2 - x^2)`

`A' = (4r^2 - 8x^2)/sqrt(r^2 - x^2)`

This will have critical numbers when

`0 = 4r^2 - 8x^2`

`8x^2 = 4r^2`

`x^2 = 1/2r^2`

`x = 1/sqrt(2)r`

The value of `y` will be given by `y = sqrt(r^2 - (1/sqrt(2)r)^2) =sqrt(1/2r^2) = 1/sqrt(2)r`

Thus the shape will be a square of dimensions `1/sqrt(2)r` by `1/sqrt(2)r`, giving a maximum area of `1/2r^2`

Hopefully this helps!