Find the equation of the lines tangent to the circle at point where x=3 x²+y²-14x+4y+33=0?
2 Answers
Explanation:
I'm going to do this using a trick that lets us do calculus on algebraic curves with only Algebra I. Let
The tangent at
We'll do the algebra, our goal being a polynomial in the small differences
Since
What we've done here is to generate what's called the Taylor expansion of
That's the equation for the tangent at
The question asks for the equations when
Plugging these in we get two tangent lines:
I'm going to post then I'll check these with the Socratic
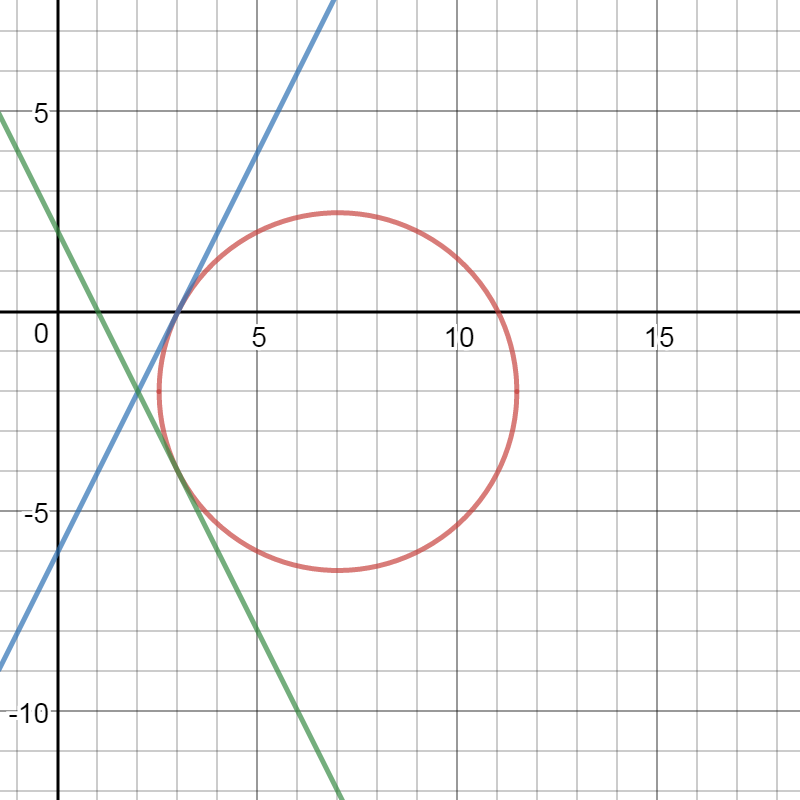
Here's the equation I'm going to feed the grapher to plot all these at once:
graph{0=(2x - y-6)(2x + y-2)( x^2 + y^2 - 14x + 4y + 33)(x-3) [-4.3, 15.815, -6.83, 3.23]}
Not the best graphing program ever, but we see we got the correct solution.
Explanation:
Using implicit differentiation.
Thus the slope of any point
We are asked to find the tangents where
At
The slope of the tangent at
The slope of the tangent at
We can see the circle and its tangents at