Find the equation of the tangent to the curve #x + xy + y = 5# at #x = 5# help?
2 Answers
Explanation:
Start by finding the y-value:
#5 + 5y + y = 5#
#6y = 0#
#y = 0#
Now we find the derivative using implicit differentiation.
#1 + y + x(dy/dx) + dy/dx = 0#
#y + x(dy/dx) + dy/dx = -1#
#x(dy/dx) + dy/dx = -1 - y#
#dy/dx(x + 1) = -1 - y#
#dy/dx = (-1 - y)/(x + 1)#
#dy/dx= -(y + 1)/(x + 1)#
At
#dy/dx= -1/6#
Now use point-slope form to find the equation:
#y - y_1 = m(x - x_1)#
#y - 0 = -1/6(x - 5)#
#y = -1/6x +5/6#
Hopefully this helps!
Explanation:
Begin by finding the y coordinate at
The point of tangency is
Compute the first derivative of the curve:
The slope, m, of the tangent line is the first derivative evaluated at the point
Use the point-slope form for the equation of a line:
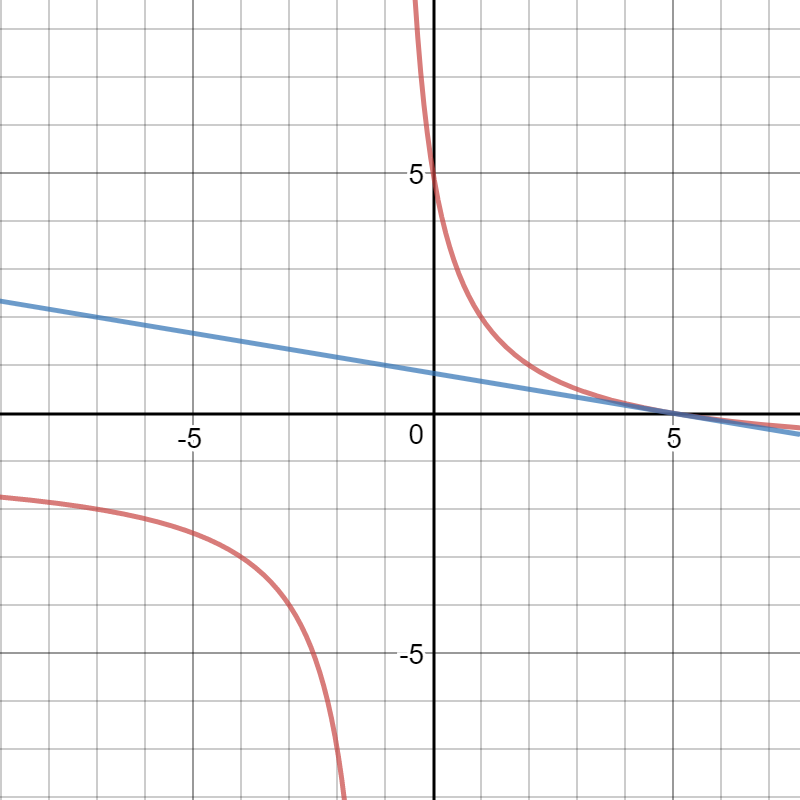
Here is the a graph of the curve and the tangent line: