Find the limit please?
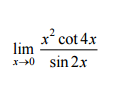
2 Answers
Explanation:
We can use the first few terms of the various Taylor Series here:
Differentiate that to get the
Replace
Explanation:
Start by simplifying the expression considering that:
so:
Now we have:
The second term is continuous in
so:
and using the limit:
we can conclude:


