Find the minimum distance between the curve #y^2 = 4ax# & #x^2 + y^2 -12x + 31=0#?
The vale of a is 1.
The vale of a is 1.
3 Answers
The points are
Explanation:
As
Now,
The distance between
or
This distance willbe minimum when
i.e.
Of these while distance of
Another way could be to find a normal to parabola which passes through the center of circle
As parametric form of equation of parabola is
If this passes through
Hence the points are
graph{(y^2-4x)(x^2+y^2-12x+31)=0 [-10, 10, -5, 5]}
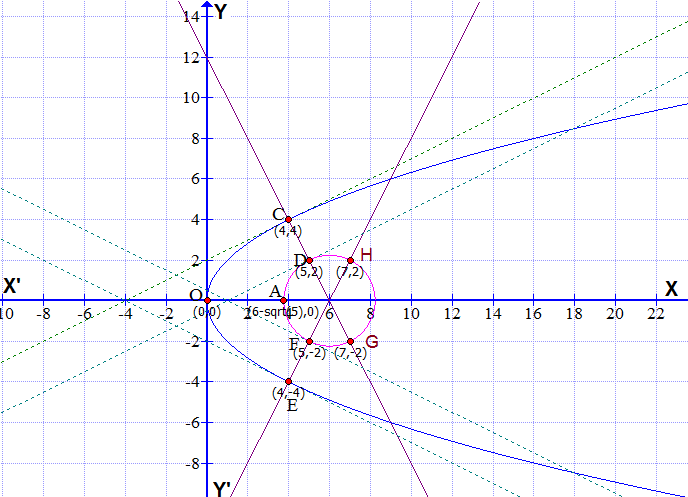
Given equations of conics are
* Parabola
* Circle
So coordinates of the center of the circle
Now to find out the minimum distance between them we can apply our simple geometric logic that in approaching towards a circle from any point outside circle, the distance covered will be minimum if approach remains directed towards its center.
Hence distance (D) of any point (para-metrically
So
Alternative Metod .
Minimum distance between the conics is the minimum length of the line segment in between them on the common normal of the two conics.
The coordinates of any point on the given parabola
So slope of the normal will be
The equation of the normal will be
Every normal of a circle passes through its center. So the equation of common normal should pass through the center of the circle.
Hence we can find the possible values of
So we get three values of
The equations of common normals are
1) Passing through
2) Passing through
3) Passing through
Solving [2] and [3] we get
So length of the line segment on common normal passing through
Solving [2] and [4]
We get
and corresponding values of y coordinates are
So the common normal passing through C(4,-4) will intersect the circle at
Here the distance between the conics along [4]
Solving [2] and [5]
We get
and corresponding values of y-coordinates are
So the common normal passing through E(4,-4) will intersect the circle at
Here the distance between the conics along [5]
Hence minimum distance between two conic is
Using the so called Lagrange Multipliers
Calling
and
then
The stationary conditions are
Solving for
and the minimum is


