Question

Find the net torque and angular acceleration of the bar?

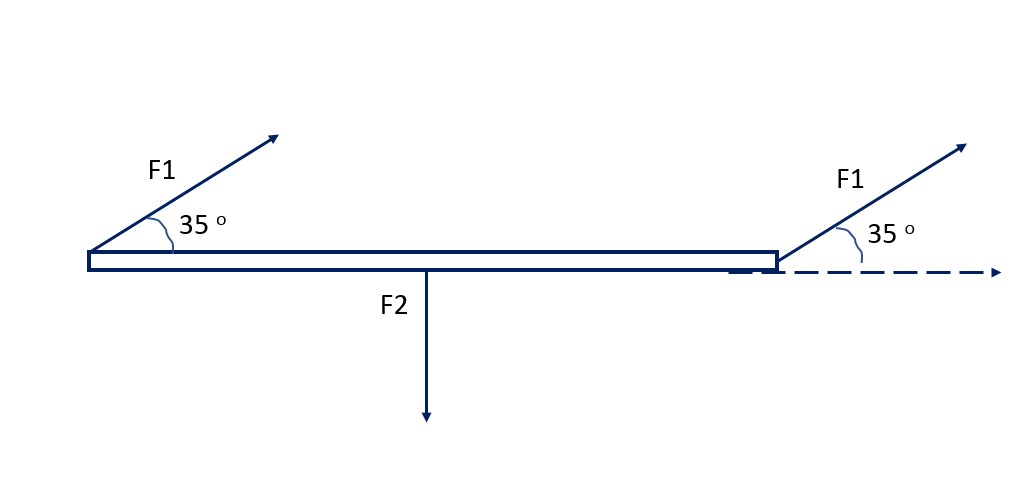
The drawing shows a bar lying on the surface of a horizontal table top. The bar is pivoted at the left end and is free to rotate with negligible friction in the horizontal plane of the table-top about the axis through the end. The bar is 2.0m long and has a mass of 0.60 kg.

The forces are as follows:
F1 = 14.0 N (at the pivot)
F2 = 12.0 N (at the 1.25m mark perpendicular to the bar)
F3 = 14.0 N (at the 2.0m mark)

Answer 1

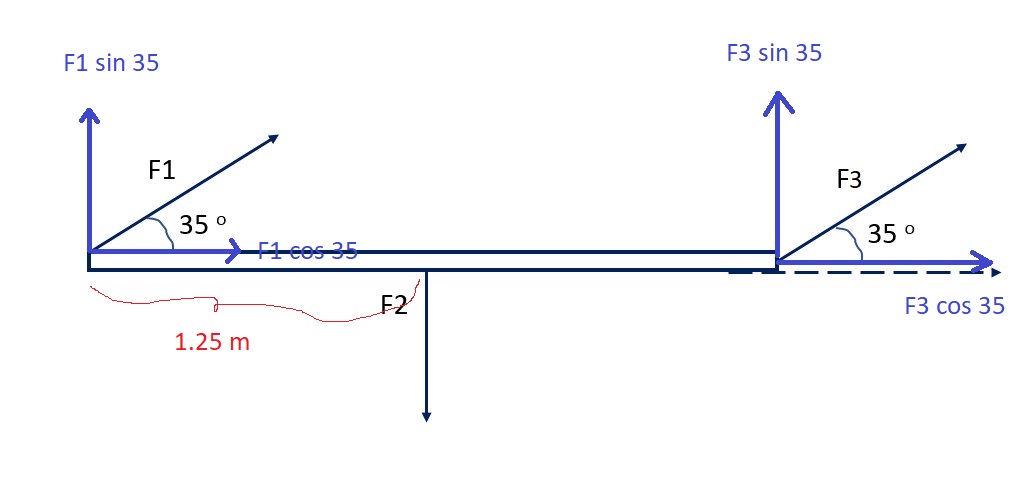
Dividing forces `F1` and `F2` into perpendicular components.

Clearly,`F1 cos 35` and `F3 cos 35` can't produce rotation of the rod as,the angle between the force and distance vector is zero.

So,only `sin` components can cause rotation.

Now,considering torque about the pivoted point,and taking the direction of the torque coming out of the plane of the page to be positive, we can write,

`-r_1*F_2 + r_2*F_3 sin 35 = I alpha` (where, `I` is the moment of inertia,for a rod about an axis passing through one end is `(ml^2)/3` and `alpha` is the angular acceleration)

Given, `r_1 =1.25,r_2=2,F_2=12,F_3=14`

So,net torque acting is `(-15+16.06) N.m` or, `1.06 N.m` Direction is along our chosen direction.

Now, `1.06 = (ml^2)/3*alpha`

Given, `m =0.60 ,l=2`

So, `alpha = 1.325 (rad)/s^2`

Note,here the pivoted point should have enough ability to pull the rod with a force of `(F_1 cos 35+F_3 cos 35)` as there is no force to balance them.