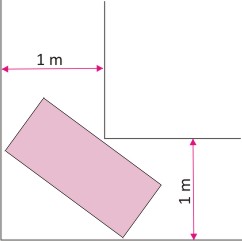
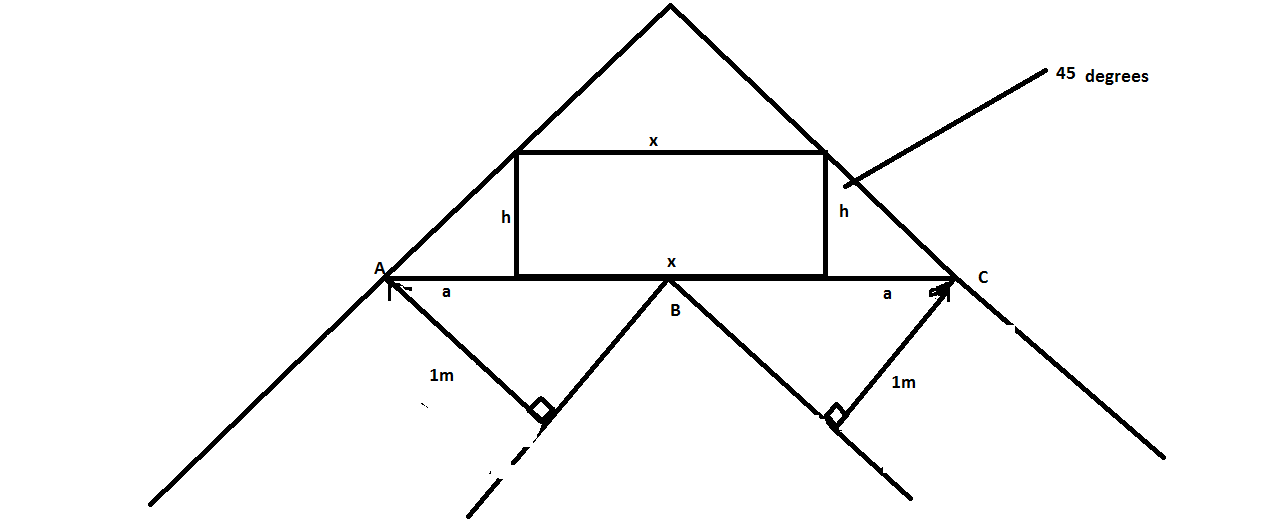
From the sketch it is seen that the length AB = BC = #sqrt2# [ by Pythagoras] since the 'tightest' position the rectangle can be in is when it's base is at 45 degrees to the sides of the #1 mtr # corridor that contains it.
Let length of base of rectangle =#x# and have a height [ or width]of #h#.
Area of rectangle will equal #xh#.........#[1]#. From the sketch, it is seen that #[2sqrt2-x]=2a# ,........ie, #a = [[2sqrt2-x]]/2#.........#[2]#.
Noting the small right angled triangle whose base is #a# and whose height #h#.
Tan #pi/4# = #a/h#, and so from .......#[2]#, and after substituting for #a# #a=[[2sqrt2-x]]/2#
#h# = #[[2sqrt2-x]]/2#,[ since tan #pi/4=1]# so from ........#[1]# area of rectangle= #[x][2sqrt2-x]/2#
= #sqrt2[x]#-#x^2/2#. Differentiating this expression, #d/dx= sqrt2-x#. This expression must equal zero for max/ min, i.e, #x=sqrt2#. and substituting this value for #x# into the expression for #h# in terms of #x# will give a value of #h# = #sqrt2/2#. The second derivative is negative = -#1# [ which is negative whatever the value of #x#]. This confirms that the #x= sqrt2# will maximise the area of the rectangle.
I hope this was helpful and I believe it is correct.