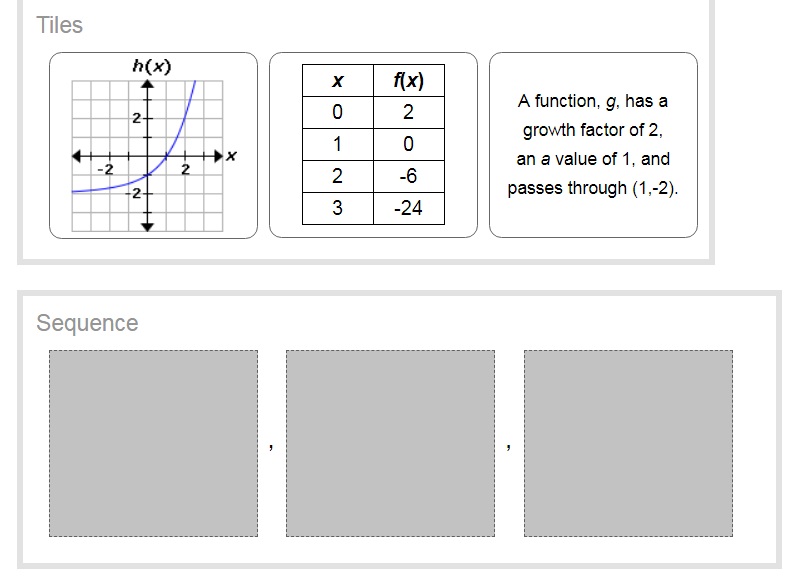
Find the y-intercept of each exponential function and order the functions from least to greatest y-intercept. ?
1 Answer
Tile 1 - Tile 3 - Tile 2
or
Tile 3 - Tile 1 - Tile 2
Explanation:
Tile One:
The
Tile Two:
The coordinates of a
Thus, in the table, the
Tile Three:
If we put the explanation into a function, it would become:
If we inserted the coordinates into the function that we've created, we get:
and now, we can complete the function to get:
To find the
Final answer:
Now we can just arrange the tiles in order of the values of the
Thus, the order is:
Tile 1 - Tile 3 - Tile 2
or
Tile 3 - Tile 1 - Tile 2
Hope that makes sense!

