For real gases, how does a change in pressure affect the ratio of PV to nRT?
1 Answer
It depends on the gas. The ratio of
#Z = (PV)/(nRT)#
-
When
#Z > 1# , the molar volume of the gas is larger than predicted by the ideal gas law, so the gas's repulsive intermolecular forces dominate. -
When
#Z < 1# , the molar volume of the gas is smaller than predicted by the ideal gas law, so the gas's attractive intermolecular forces dominate. -
When
#Z = 1# , the gas is ideal.
In principle, higher pressures (and lower temperatures) should make the gas behave more like a real gas (interacting, "sticky" particles).
But higher pressures alone don't give rise to a clear relationship with
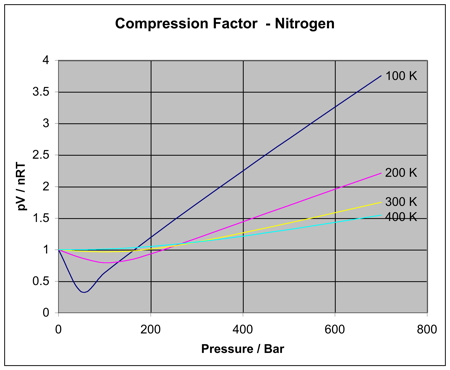
You can see that at higher temperatures, the curve for

