Question

For the atomic shell with quantum number n = 1, how many sub-shells are possible where each sub-shell has a different value of the angular momentum quantum?

Answer 1

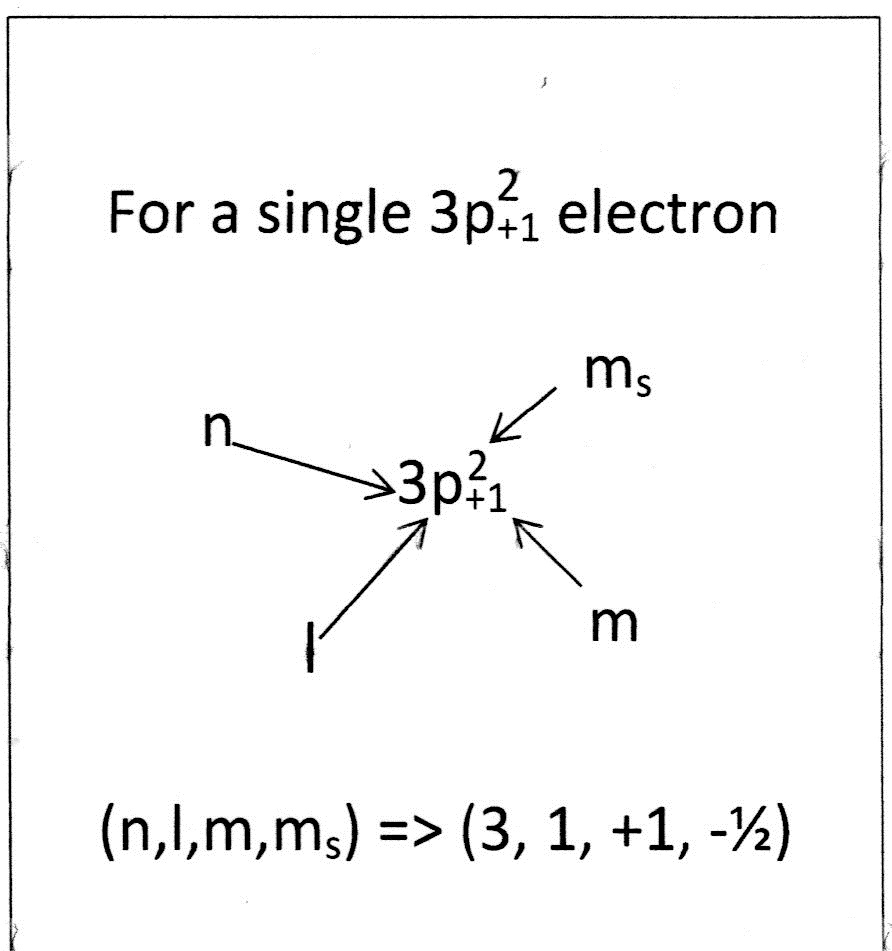
For n = 1 there is only one sub-shell => l = s = 0 & m = 0

Explanation:

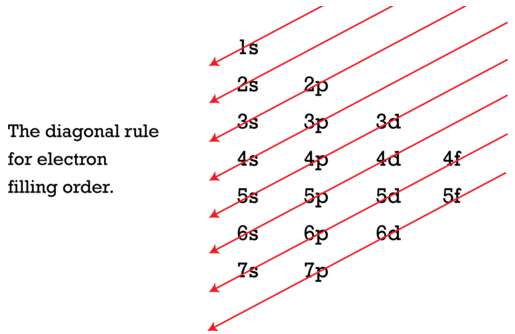
Using the Aufbau Diagram and the 'building up sequence' of adding electrons into electronic orbitals; that is, electrons enter the lowest available energy level during the sequential building up the electronic cloud.

For a given Principle Quantum Number (n), the number of orbitals (or, suborbitals) associated with that energy level equals the value of n. That is, for

n = 1 => 1 sublevel => 1s
n = 2 => 2 sublevels => 2s 2p
n = 3 => 3 sublevels => 3s 3p 3d
n = 4 => 4 sublevels => 4s 4p 4d 4f
n = 5 => 5 sublevels => 5s 5p 5d 5f (5g)
n = 6 => 6 sublevels => 6s 6p 6d (6f)(6g) (6h)
n = 7 => 7 sublevels => 7s 7p (7d) (7f) (7g) (7h) (7i)*
undiscovered
number values s => 0 p => 1 d => 2 f = 3

For the Angular Momenum QN (or, Magnetic QN) => number of orientations per known sublevels...

s => 1 => `color(white)((m)(m)(m)(m))(s_0)`
p => 3 => `color(white)(()()()()())(p_(-1)) (p_(0)) (p_(+1))`
d => 5 => `color(white)(()())(d_(-2))(d_(-1))(d_(0))(d_(+1))(d_(+2))`
f => 7 => `(f_(-3))(f_(-2))(f_(-1))(f_(0))(f_(+1))(f_(+2))(f_(+3))`

Spin QN ...
(m_+1/2) => clockwise spin
(m_ -1/2) => counterclockwise spin

Order of filling is frequently illustrated as follows in the Aufbau Diagram ...

For the 4 quantum numbers `(n, l, m, m_s)` for a single 3p electron...