For the z-test statistic 1.34, how do you compute the p-value assuming that the hypothesis test is a one-tailed test?
1 Answer
Explanation:
The
From Wolfram Mathworld, the values of the normal cumulative distribution function cannot
"...be expressed in terms of finite additions, subtractions, multiplications, and root extractions, and so ... must be either computed numerically or otherwise approximated."
Typically, one uses a computer or looks the value up in a table like this one from https://statistics.laerd.com.
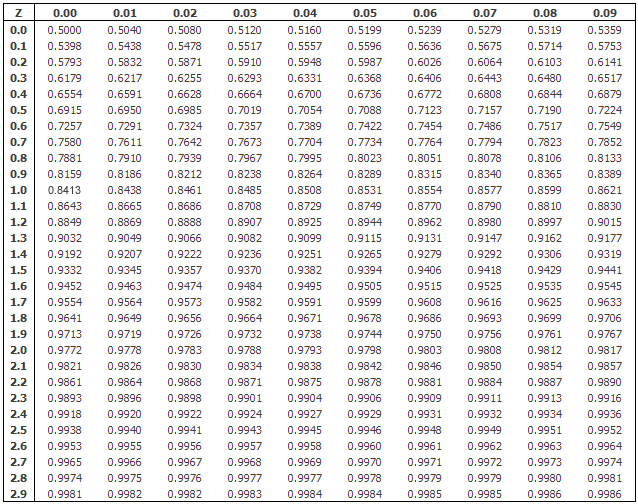
From this table we can see that a z value of 1.34 corresponds to a
One can also use Microsoft Excel to calculate
=1-NORMSDIST(z-statistic value)
For example, when I put this formula in a cell
=1-NORMSDIST(1.34)
The cell displays
There are also free online calculators like this one .

