Question

For what value of `k` will `x+k/x` have a relative maximum at `x=2`?

Answer 1

There is no such `k`.

Explanation:

Let `f(x) = x+k/x`

the `f'(x) = 1-k/x^2`

In order for `f` to have `2` as a critical number we must have `k=4`.

However, `1-4/x^2` is negative on `(0,2)` and positive on `(2,oo)`, so `f` has a relative MINIMUM at `x=2`.

Answer 2

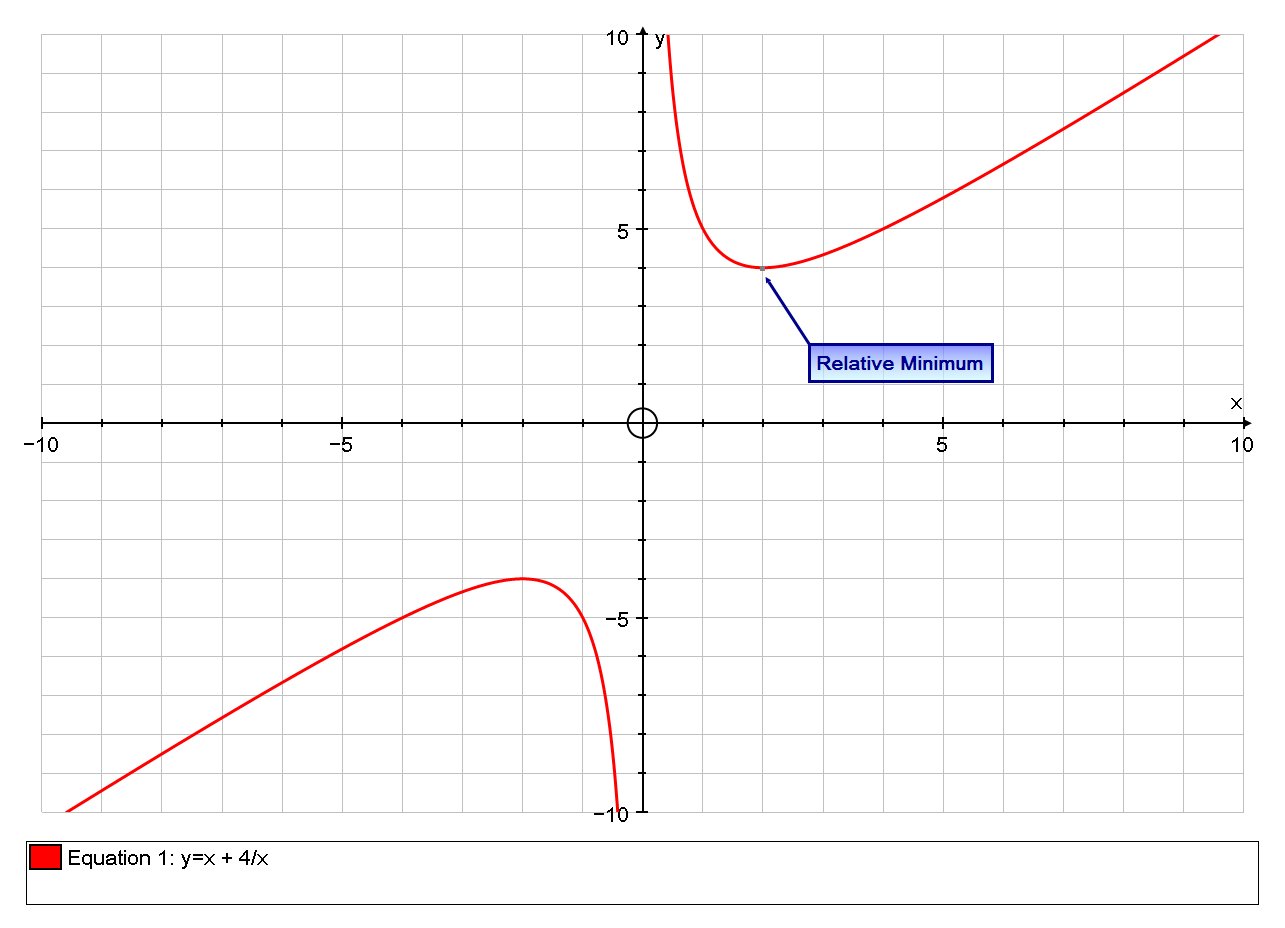
There is a relative minimum when `x=2` with `k=4`, but there is no possible value of k which gives a relative maximum when `x=2`

Explanation:

Let

`f(x) = x+k/x`

Then differentiating wrt `x` we get

`f'(x) = 1 - k/x^2`

And differentiating again wrt `x` we get:

`f''(x) = (2k)/x^3`

the `f'(2) = 1-k/4`

At a maximum or minimum we require `f'(x) =0`, so for a maximum when `x=2` we must have `f'(2)=0`

`f'(2)=0 => 1 - k/2^2=0`
`:. 1-k/4 = 0`
`:. k = 4`

So When `k=4 => f'(x)=0` when `x=2` giving a single critical point

Now let's find the nature of this critical point. With `k=4` and `x=2`

`f''(2) = ((2)(4))/2^3 > 0`, Hence this a relative minimum