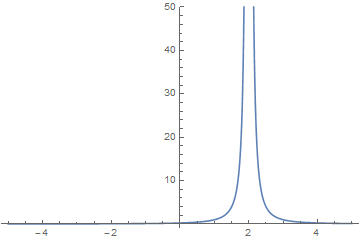
For what values of x, if any, does #f(x) = 1/(x^2-4x+4) # have vertical asymptotes?
1 Answer
Feb 6, 2016
Explanation:
To find the vertical asymptotes we have to find for which values the denominator is equal to 0. Simply set the polynomial on the denominator to 0 then solve for
Thus there is one vertical asymptote at
Here is a graph of the function, the vertical asymptote is clearly indicated by a steep incline towards