For what values of x is #f(x)=(5x-1)(x-5) (2x+3)# concave or convex?

Question

1114 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-01-13T12:26:37

Convex #color(white)(888)x in(37/30 , oo)#

Concave #color(white)(888)x in (-oo , 37/30)#

We can test for concavity using the second derivative. If:

#(d^2y)/(dx^2)>0# convex ( concave up )

#(d^2y)/(dx^2)<0# concave ( concave down )

#(d^2y)/(dx^2)=0# concave/convex or point of inflection. This would have to be tested.

#f(x)=(5x-1)(x-5)(2x+3)#

It will make the differentiation easier if we expand this:

#(5x-1)(x-5)(2x+3)=10x^3-37x^2-68x+15#

The second derivative is the derivative of the first derivative, so:

#dy/dx(10x^3-37x^2-68x+15)=30x^2-74x-68#

#(d^2y)/(dx^2)=dy/dx(30x^2-74x-68)=60x-74#

#:.#

#60x-74>0# , #x>37/30#

Convex #color(white)(888)x in(37/30 , oo)#

#60x-74<0# , #x<37/30#

Concave #color(white)(888)x in (-oo , 37/30)#

GRAPH:

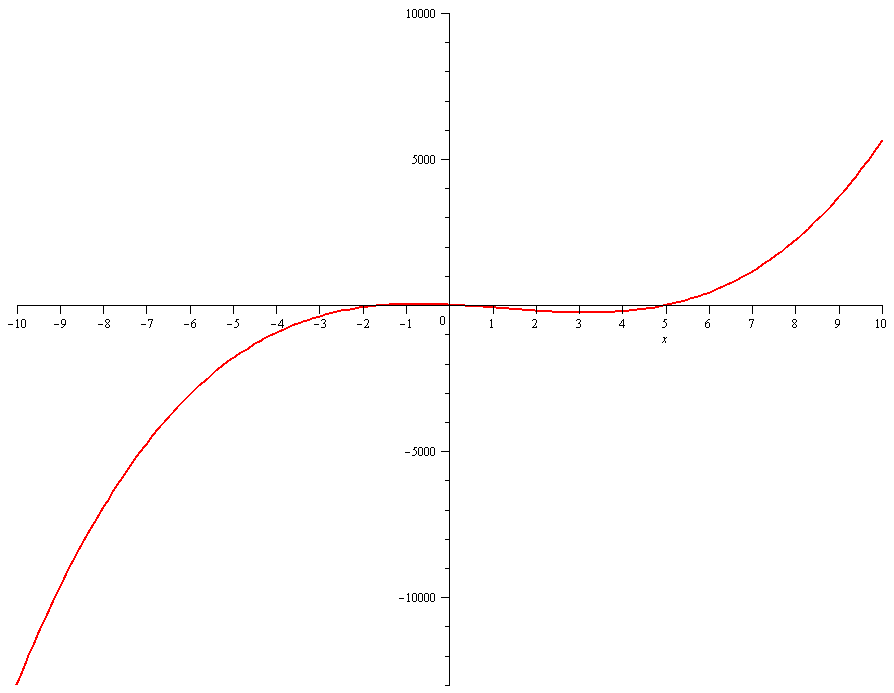
enter image source here