For what values of x is #f(x)=-x^4+4x^3-2x^2-x+5# concave or convex?
1 Answer
Jun 1, 2016
Explanation:
For
For
we have
If
otherwise if
Extracting the roots of
we get
blue
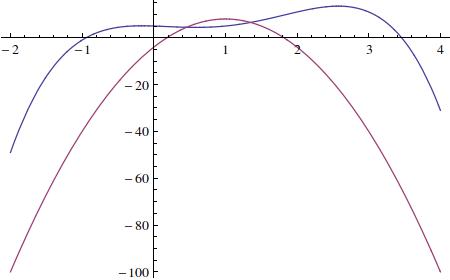
For
For
we have
If
otherwise if
Extracting the roots of
we get
blue
