Question

For what x an y is `y / ( x^3 + 3 )^2 > 2/(x/y-y-3)`?

Answer 1

See below

Explanation:

Compacting the inequality we have

#-(y (18 - x + 12 x^3 + 2 x^6 + 3 y + y^2))/((3 + x^3)^2 (x - 3 y - y^2) )>0# or
`-(y (18 - x + 12 x^3 + 2 x^6 + 3 y + y^2))/(x - 3 y - y^2)>0`
because

`(3 + x^3)^2 ge 0 forall x in RR`

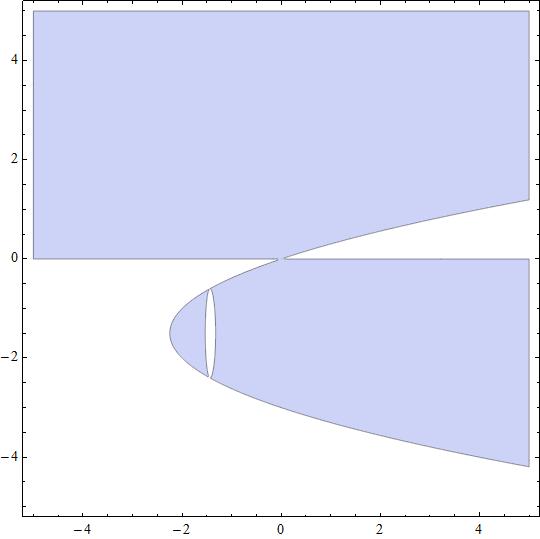
The feasible set frontier is composed of

`f_1(x,y)=-y = 0`
`f_2(x,y)= 18 - x + 12 x^3 + 2 x^6 + 3 y + y^2=0`

and

`f_3(x,y) =x - 3 y - y^2=0`

The feasible region interior is the set of points `{x,y}` obeying

`f_1(x,y)f_2(x,y) > 0 and f_3(x,y)>0`

or

`f_1(x,y)f_2(x,y) < 0 and f_3(x,y)<0`

This set is shown in the attached figure in light blue