Given point (24,7) how do you find the distance of the point from the origin, then find the measure of the angle in standard position whose terminal side contains the point?
1 Answer
Mar 4, 2018
Polar coordinates of
Explanation:
Given Point
To find distance of A from origin
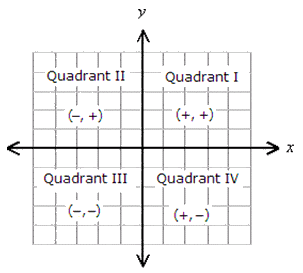
Both x & y coordinates are positive and hence point A is in first quadrant.
Coordinates of origin is
Distance formula to calculate the distance between two points is
Since one point (origin) has coordinates (0,0),
To find the measure of angle
Polar coordinates of
