Question

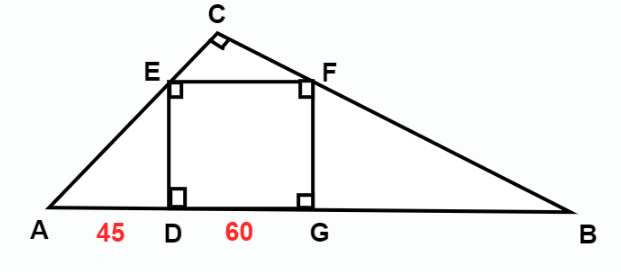
Given that, `\overline{AD}=45` and `\overline{DG}=60`, find the lengths of other line segments in this right triangle `\triangle ABC` given that the `DEFG` is a square?

Answer 1

`DE = EF = FG = 60`

`AE = 75, EC = 36, BG = 80, BF = 100, CF = 48`

Explanation:

`DE = EF = FG = 60` as DEFG is a square

`tan A = 60 / 45 = (4/3)^c`

`hat A = tan ^(-1) (4/3) = 0.9273`

`hat B = pi - pi/2 - 0.9273 = 0.6435`

`BF = sqrt((BG)^2 + (GF)^2) = sqrt(80^2 + 60*3) = 100`

`hat A = hat E = 0.9273` (corresponding angles)

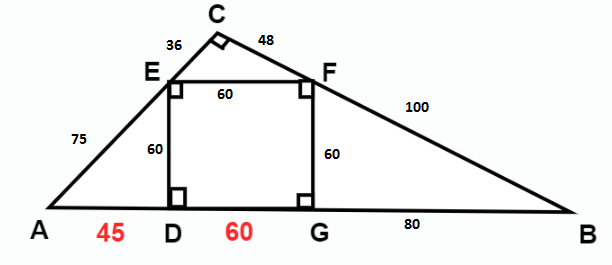
In triangle CEF,

`CE = EF cos hat E = 60 cos 0.9273 = 36`

`CF = EF sin hatE = 60 sin 0.9273 = 48`

In triangle BFG,

`BG = (FG) / tan hatB =`60 / tan (0.6435) = 80#

In triangle AEF,

`AE = sqrt((AD)^2 + (DE)^2) = sqrt(45^2 + 60^2) = 75`

Verification :

In right triangle ABC,

`AB = sqrt((AC)^2 + (BC)^2)`

`AB = = 45 + 60 + 80 = color(green)(185`

`sqrt((AC)^2 + (BC)^2) = sqrt((75+36)^2 + (100 + 48)^2) = color(green)(185`

Hence Proved.

Answer 2

Please see below.

Explanation:

.

Because `DEFG` is a square, it has all equal sides:

`DE=EF=FG=DG=60`

Because `EF` and `|AB` are parallel,

`/_CFE=/_CBA` and `/_CEF=/_CAB`

This means that by virtue of Angle Angle theorem:

`DeltaADE~=DeltaECF`

`DeltaFGB~=DeltaECF`

`DeltaACB~=DeltaCEF`

Therefore, all four right angle triangles are similar which mean the ratios of their corresponding sides are equal.

`(AD)/(FG)=(ED)/(GB)`

`45/60=60/(GB)`

`GB=3600/45=80`

`AB=AD+DG+GB=45+60+80=185`

`(AE)^2=(AD)^2+(DE)^2`

`(AE)^2=(45)^2+(60)^2=2025+3600=5625`

`AE=75`

`(DE)/(CF)=(AE)/(EF)`

`60/(CF)=75/60`

`CF=3600/75=48`

`(AD)/(CE)=(AE)/(EF)`

`45/(CE)=75/60`

`CE=2700/75=36`

`AC=AE+EC=75+36=111`

`(ED)/(GB)=(AE)/(FB)`

`60/80=75/(FB)`

`FB=6000/60=100`

`CB=CF+FB=48+100=148`