The solution of ax2+bx+c=0 is given by x=−b±√b2−4ac2a
However, if equation is divided by a, it becomes of the form x2+bx+c=0, whose solution is x=−b±√b2−4c2
and sum of roots is −b and product is c,
and in x2+4x−32=0, product of roots would be 32 and as its sign is negative, difference of roots is 4, with smaller root being positive and larger root being negative.
We can follow the following geometric construction, if in x2+bx+c=0, c<0 and signs of roots are opposite. If b<0 smaller root is negative (and larger root is positive) and if b>0, larger root is negative ((and larger root is negative)).
In such cases, we draw a circle of diameter equal to difference of roots (i.e. b) and then a tangent CP equal to square-root of product of roots (i.e. √c) and then join P to the center of circle as shown, then BP and DP represent the two roots of the equation .
So when draw a circle of diameter 4 units and draw a tangent of length equal to √32 and join as shown in figure, we will find BP and DP as 4 and 8 respectively and hence roots are 4 and −8.
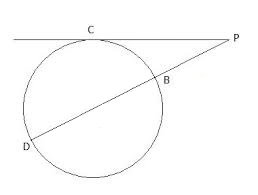
If in x2+bx+c=0, c>0, we can follow the following geometric construction. In this case, if b<0 both roots are positive and if b>0, both roots are negative.
As in such cases, sum of roots and product of roots are known, one can draw a circle with diameter equal to sum of the roots i.e. b, (AB in figure below) and then draw a line parallel to its diameter at a distance equal to square-root of product of roots i.e. √c, (CD in figure below with EF=√c), cutting circle at E. Now draw a perpendicular EF⊥AB. Then AF and BF represent the two roots.
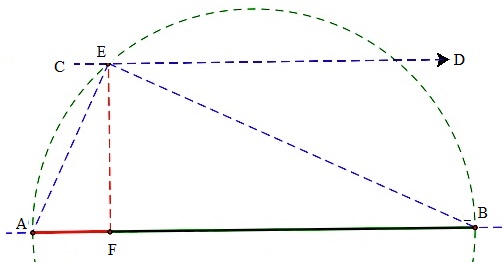
In case any of these construction is not possible, we may have determinant b2−4ac<0 and roots are complex.


