 drawn
drawn
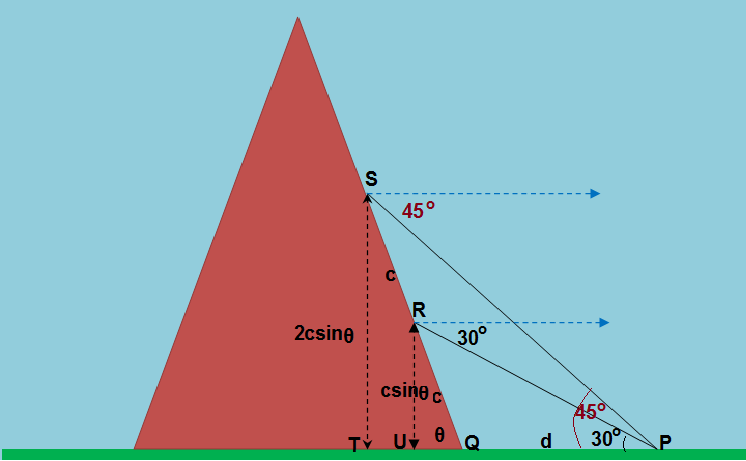
The above figure explains the situation described in the given problem.
Q->"the starting point"
P->"the point at a distance d m from from Q"
R->"the point from which angle of depression of P is " 30^@
S->"the point from which angle of depression of P is " 60^@
Let the angle of inclination of slope of the mountain be theta
Here QR=c and QS=2c
So RU=csintheta ;QU=c costheta
and ST=2csintheta ;QT=2c costheta
Now (RU)/(PU)=tan30^@
=>(RU)/(QU+QP)=tan30^@
=>(csintheta)/(c costheta+d)=1/sqrt3
=>c costheta+d=sqrt3csintheta......[1]
Again (ST)/(PT)=tan45^@
=>(ST)/(QT+QP)=tan45^@
=>(2csintheta)/(2c costheta+d)=1
=>2c costheta+d=2csintheta......[2]
Subtracting (1) from (2) we get
2csintheta-sqrt3csintheta=c costheta
=>csintheta(2-sqrt3)=c costheta
=>tantheta=1/(2-sqrt3)=2+sqrt3
=>theta =75^@
Alternative method
In Delta PQR,angleQRP=(theta-30^@)
So c/(sin30^@) =d/sin(theta-30^@)
=>2c=d/sin(theta-30^@)
And in Delta PQS,angleQSP=(theta-45^@)
So (2c)/(sin45^@) =d/sin(theta-30^@)
=>2sqrt2c=d/sin(theta-45^@)
Hence sqrt2sin(theta-45^@)=sin(theta-30^@)
=>sintheta-costheta=sqrt3/2sintheta-1/2costheta
=>2sintheta-2costheta=sqrt3sintheta-costheta
=>tantheta=1/(2-sqrt3)=2+sqrt3=tan75^@
Please note
tan75^@=tan(45^@+30^@)
=(tan45^@+tan30^@)/(1-tan45^@tan30^@)
=(1+1/sqrt3)/(1-1/sqrt3)
=(sqrt3+1)/(sqrt3-1)
=(sqrt3+1)^2/((sqrt3)^2-1^2)
=(4+2sqrt3)/2=2+sqrt3
 fiitjee ftre exam
fiitjee ftre exam  fiitjee ftre exam
fiitjee ftre exam  drawn
drawn 
