Help please?!

Question

1730 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-07-15T14:29:42

The answers are #(b)=4.95ms^-1# and #(c)=495ms^-1#

Part #(a)#

When the shot is released, there is a recoil of the gun, but momentum is conserved

#m_gv_g=-m_bv_b#

The gun recoils in the opposie direction.

Part #(b)#

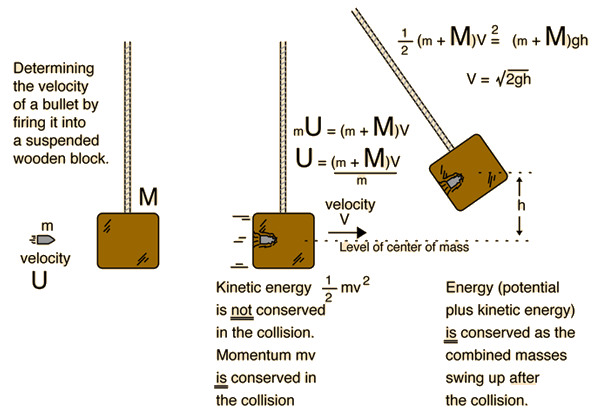
enter image source here

The height #h=1.25m#

Mass of the bullet is #m=0.005kg#

Mass of the target is #M=0.495kg#

Let the speed of the bullet #+# target be #=vms^-1#

Then,

#KE=PE#

#1/2*(m+M)v^2=(m+M)gh#

#v=sqrt(2gh)=sqrt(2*9.8*1.25)#

#=sqrt24.5#

#=4.95ms^-1#

Part #(c)#

Let the velocity of the bullet before hitting the target is #=ums^-1#

#mu+M*0=(m+M)*v#

#u=(m+M)/m*v#

#=(0.495+0.005)/0.005*4.95#

#=0.5/0.005*4.95#

#=495ms^-1#