How are the conditions of pressure and temperature shown on a [phase] diagram at which two phases coexist in equilibrium?
1 Answer
Well, luckily for us, phase diagrams are made to be straightforward to read. The curves are literally the lines of two-phase coexistence.
They indicate one degree of freedom (i.e. parallel to the curve at each instantaneous displacement), in accordance with the Gibbs' phase rule.
Consider the phase diagram of water:
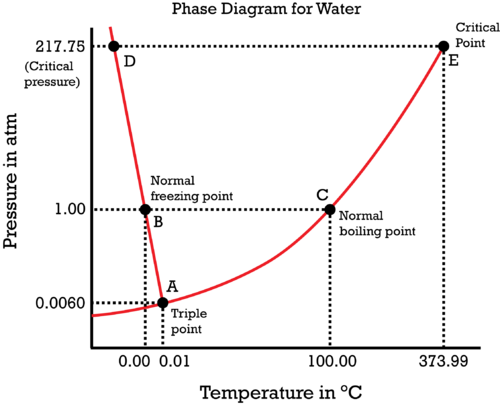
If you are unsure how many phases there are in a given region on a phase diagram, refer to the Gibbs' phase rule to check:
#bb(f = c - p + 2)#
#f# is the number of degrees of freedom, i.e. the number of coordinate directions you are allowed to move in a phase diagram without moving out of the bounds of consideration.#c# is the number of components in the substance (could be a solution full of electrolytes... could be interacting).#p# is the number of phases.
Below are example calculations for cases we should already be able to verify physically.
TEST CHECK 1: TRIPLE POINT
For example, consider the triple point of water at
#f = 0# , because you can't move around in a triple point in any way, unless you are no longer at the triple point.#c = 1# for pure substances, because there is only one of itself in itself.
This indicates that the number of phases at a triple point is:
#bb(p) = c + 2 - f = 1 + 2 - 0#
#= bb3# phases in equilibrium at the triple point.
And in fact, that's why it's called a triple point, because three phases coexist at a triple point.
TEST CHECK 2: COEXISTENCE CURVE
Or, consider the liquid-vapor coexistence curve,
#f = 1# , because if you move parallel to the curve for each instantaneous displacement, you won't move off the curve.#c = 1# , because our water sample is assumed to be a pure substance.
And we get:
#bb(p) = c + 2 - f = 1 + 2 - 1#
#= bb(2)# phases in equilibrium with each other, as expected.
TEST CHECK 3: SINGLE-PHASE REGION
Or, consider just being in a single-phase region, like at
#f = 2# , because you can move in spirals if you wanted, which requires hybridizing two particular coordinate directions, while still staying in the same two-dimensional region.#c = 1# , and we know why at this point.
So,
#bb(p) = c + 2 - f = 1 + 2 - 2#
#= bb(1)# phase exists by itself, which we already said... it's the liquid phase.

