How are the Pythagorean Theorem and the Distance Formula related?
2 Answers
If we consider what the distance formula really tells you, we can see the similarities. It is more than just a similar form.
The distance formula is commonly seen as:
#D = sqrt((x_1 - x_2)^2 + (y_1 - y_2)^2)#
We commonly write the Pythagorean Theorem as:
#c = sqrt(a^2 + b^2)#
Consider the following major points (in Euclidean geometry on a Cartesian coordinate axis):
- The definition of a distance from
#x# to#pmc# is#color(green)(|x-c|)# . - There is the relationship where
#sqrt((x-c)^2) = color(green)(|x-c|) = x-c " AND " -x+c# - The distance from one point to another is the definition of a line segment.
- Any diagonal line segment has an
#x# component and a#y# component, due to the fact that a slope is#Deltay"/"Deltax# . The greater the#y# contribution, the steeper the slope. The greater the#x# contribution, the flatter the slope.
What do you see in these formulas? Have you ever tried drawing a triangle on a Cartesian coordinate system? If so, you should see that these are two formulas relating the diagonal distance on a right triangle that is composed of two component distances
Or, we could put it another way through substitutions based on the distance definitions above. Let:
#x_1 - x_2 = pma#
#y_1 - y_2 = pmb#
(depending on if#x_1 > x_2# or#x_1 < x_2# , and similarly for#y# .)
Now what do you see? An equivalence.
#D = color(blue)(sqrt((pma)^2 + (pmb)^2)) = c = color(blue)(sqrt(a^2 + b^2))#
In short, the distance formula is a formalization of the Pythagorean Theorem using
Essentially, they are "the same thing". As long as we stay in the context of Euclidean Geometry (not in the contemporary sense), the distance formula can be derived from the Pythagorean Theorem.
Explanation:
The distance formula makes sense in a coordinate context. It's used to compute the distance between two points in an orthogonal coordinate system (i.e. a plane with a coordinate system such that).
First of all, let's compute the distance between
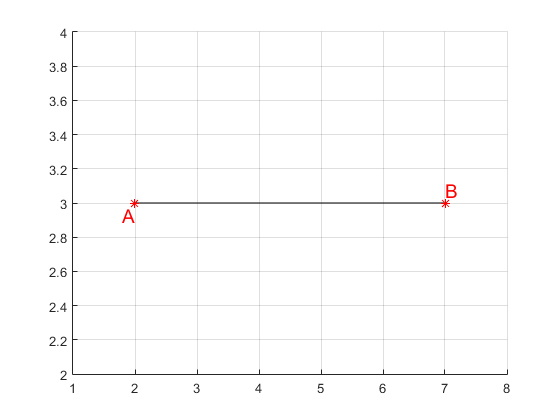
This is quite easy, because the two points lie on the horizontal line
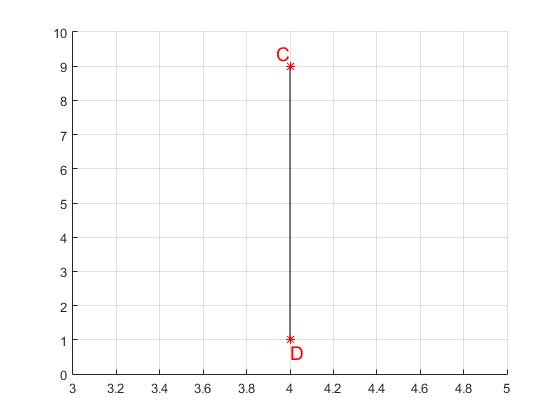
Similarly the distance between
Now we have all the ingredients we need. In fact, let's think about computing the distance between the points
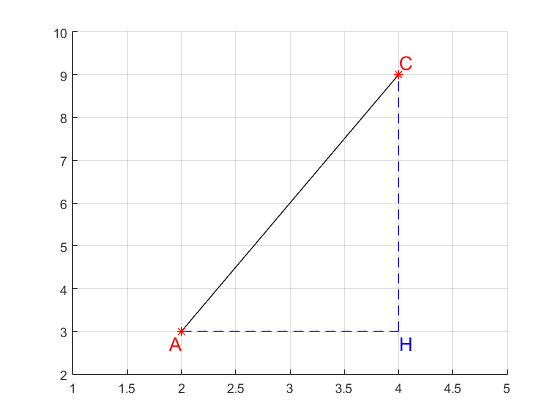
So to compute the distance between
We got rid of the absolute values because squaring a number
Now, since
NOTE:
The contemporary way of thinking of distances is significantly different. Nowadays, the definition of distance between two points deeply influences the geometry of the space you work in, and the euclidean distance (the one that corresponds to Euclidean Geometry) is just one of the (infinitely-)many possible choices. So given - for example - a plane, one has first to define how the distance is computed and from this it will automatically follow the geometry of the plane (i.e. which lines can be called "straight", which are the triangles, ...) and if the Pythagorean Theorem (or some variation of it) holds. More technical details can be found in Wikipedia's article about enter link description here .
It may seem an abstract useless thing, but it's tremendously useful: Einstein's relativity and other important sector of physics are built on this. A curious and (hopefully) easy-to-understand example is the taxicab distance .