Question

How can I determine the graph using the properties ?

Answer 1

`D`

Explanation:

We know when `f'(x)=0` this indicates a maximum or minimum point. From the table this is at `(-2, 13)` and `( 2 , -19)`. Looking at the graphs this indicates either A or D. We know for a maximum point `f''(x)<0` and for a minimum point `f''(x)>0`. From the table `f''(x)<0` at `( -2 , 13`) and `f''(x)>0` at `( 2 , -19)`. Looking at graphs of A and D. D has maximum at `( -2 , 13)` and a minimum at `( 2 , -19)`

So D is the graph represented by the table.

Answer 2

`D`

Explanation:

Alright, we take this step by step.
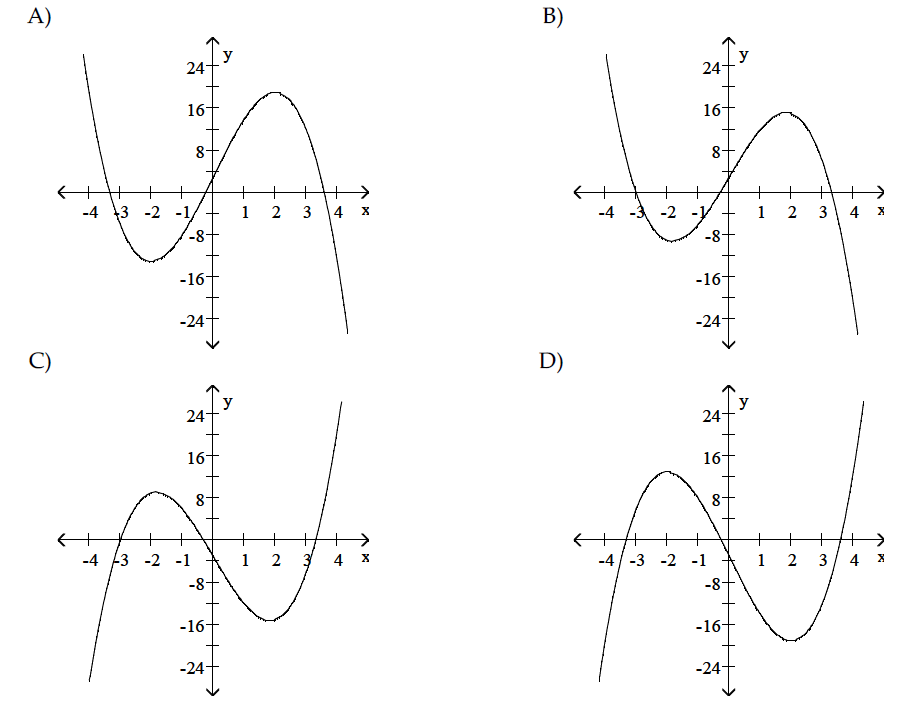
Let's try to exclude some of the graphs for `f` .

Looking at them it's easy to tell that for `x>2` we have the first two where `f` is decreasing and is concave. This doesn't satisfy one of the properties given for `f` which is ( `x>2, f'(x)>0, f''(x)>0` ) which means `f` should be increasing for `x>2` and it should be convex.

With this restriction possible graphs would be either `C` or `D`
If you look at them , they look very identical in their shape so most of the properties should be satisfied by both of the graphs. Take a close look on what's happening in these 2 graphs when `x=-2`

When `x` is `-2`, `y` should be equal to `13` with the given table which if you look it's the case on the `D` graph.
Since one of the properties doesn't satisfy the `C` graph it's enough to assume that graph `D` is the closest approximation we can get to the graph for the function `f`