How do I interpret an enthalpy diagram?
1 Answer
I assume you mean in the context of Hess's Law and the Born-Haber Cycle, which take advantage of the state function quality of enthalpy to construct a pathway for a multi-step reaction based on the enthalpies, ionization energies, and electron affinities for the individual steps.
We thus determine the energy needed to BREAK the lattice.
DETERMINING THE LATTICE ENTHALPY ONE STEP AT A TIME
Let's take an example where we calculate the lattice enthalpy (i.e. the enthalpy required to break the lattice structure and turn its constituents into gases) from the following overall reaction:
#color(green)("MgF"_2(s) -> "Mg"^(2+)(g) + 2"F"^(-)(g))#
In order to transform the molecular reactant into the atomic products, the first thing we have to do is "unform" it, i.e. reverse its formation reaction. To this we assign
"
#"MgF"_2(s) => "Mg"(s) + "F"_2(g) " >> " -DeltaH_f#
Next, we have to turn the atoms into gases, because the products are gases. We assign to this the atomization enthalpy,
#"Mg"(s) => "Mg"(g) " >> " DeltaH_"atom"#
Then, since magnesium became a cation by the removal of electrons, we must utilize the ionization energy, to which we assign
#"Mg"(g) -> cancel("Mg"^(+)(g)) + e^(-) " >> " "IE"_1#
#cancel("Mg"^(+)(g)) -> "Mg"^(2+)(g) + e^(-) " >> " "IE"_2#
#"----------------------------------------"#
#"Mg"(g) -> "Mg"^(2+)(g) + 2e^(-) " >> " "IE"_1 + "IE"_2#
Next, we move onto fluorine, which needs to be turned into two atoms instead of one diatomic molecule. We call that the bond(-breaking) enthalpy
#"F"_2(g) => 2"F"(g) " >> " DeltaH_"bond"#
The next thing we would do is notice that we still need to ionize fluorine to achieve the final form of all the products. Since fluorine will acquire electrons to become negatively charged, we assign to this process the electron affinity
Note that since we have two fluorine atoms to anionize, we must double the electron affinity, which originally accounts for only one
#2"F"(g) + 2e^(-) => 2"F"^(-)(g)" >> " 2"EA"#
THE OVERALL PATHWAY FOLLOWS HESS'S LAW
Finally, we add all this up to get:
#"MgF"_2(s) => cancel("Mg"(s)) + cancel("F"_2(g)) " >> " -DeltaH_f#
#cancel("Mg"(s)) => cancel("Mg"(g)) " >> " DeltaH_"atom"#
#cancel("Mg"(g)) -> "Mg"^(2+)(g) + cancel(2e^(-)) " >> " "IE"_1 + "IE"_2#
#cancel("F"_2(g)) => cancel(2"F"(g)) " >> " DeltaH_"bond"#
#cancel(2"F"(g)) + cancel(2e^(-)) => 2"F"^(-)(g)" >> " 2"EA"#
#"----------------------------------------"#
#color(blue)("MgF"_2(s) -> "Mg"^(2+)(g) + 2"F"^(-)(g))#
As one should expect, the intermediate reactants and electrons cancel out.
CONSTRUCTING THE "ENTHALPY DIAGRAM"
For the above enthalpies, ionization energies, and electron affinities, we have:
#-DeltaH_f = "1124 kJ/mol"# #DeltaH_"atom" = "147 kJ/mol"# #"IE"_1 + "IE"_2 = (744 + 1457)# #"kJ/mol"# #DeltaH_"bond" = "155 kJ/mol"# #2"EA" = 2*(-"328 kJ/mol")#
where we used the convention of positive for breaking interactions and negative for making interactions. From this, we could construct an "enthalpy diagram":
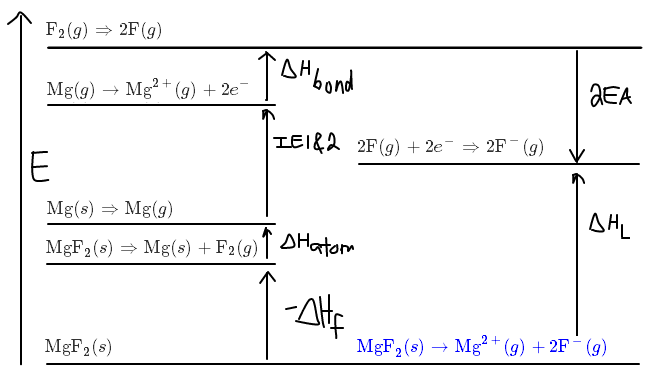
Now if we were to calculate
#color(blue)(DeltaH_"L") = stackrel("Magnesium")overbrace((DeltaH_"atom" + "IE"_1 + "IE"_2)) + stackrel("Fluorine")overbrace((DeltaH_"bond" - 2"EA")) + (-DeltaH_f)#
#= 147 + 744 + 1457 + 155 - 2*(328) + 1124#
#=# #color(blue)("2971 kJ/mol")#
This gives us the energy needed to BREAK the lattice. Normally though, the energy is listed as negative, the energy needed to FORM the lattice.

