For an initial explanation, I think it's better not to"swap" the variables in writing the inverse function. In other words, if #x# is the independent (input) variable for #f#, it will become the dependent (output) variable for #f^{-1}#. (This is important in applied problems so that the variable names have consistent meanings).
Let #y=f(x)=x^3+x+1# and let #x=f^{-1}(y)# be the inverse function of #f# (there's no need to find a formula for #f^{-1}#).
The rule for differentiating the inverse function in this context can be written in Leibniz notation as #dx/dy=1/(dy/dx)#. While this is somewhat intuitive, it is a bit sloppy because it's not clear how to use it. To be more precise, we can write the rule as #(f^{-1})'(y)=1/(f'(f^{-1}(y))#.
Note that #f'(x)=3x^2+1# and that #f(2)=2^3+2+1=11# so that #f^{-1}(11)=2#. Then the rule at the end of the paragraph above can be written as #(f^{-1})'(11)=1/(f'(f^{-1}(11)))=1/(f'(2))=1/(3*2^2+1)=1/13#. That's the answer. Notice that I took the number #11# to be a #y#-value instead of an #x#-value because I did not "swap" the #x# and #y# in writing the inverse function.
If you don't do the swapping of the variables, here's an intuitive justification of what I've done. Letting #y=f(x)# and noting that #f(2)=11# and #f'(2)=13#, we get the approximation #\Delta y\approx 13*\Delta x# when #x=2# and #\Delta x\approx 0#. This means, for instance, that #f(2.01)\approx 11+13*0.01=11.13#.
Since #Delta y\approx 13*\Delta x# in such a situation, it should make intuitive sense that #Delta x\approx 1/13*\Delta y# in essentially the same situation (thought of this time in terms of #y=11# and #\Delta y\approx 0#). This means, for example, that #f^{-1}(11.01)\approx 2 + 1/13*0.01\approx 2.00077#.
If you do swap the variables and write #y=f(x)# as well as #y=f^{-1}(x)#, then the well-known reflection property of the graphs of these functions across the line #y=x# is what gives geometric justification of what I've done.
Here's the picture in the given situation.
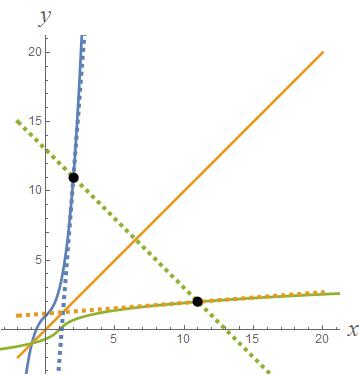
In this picture the graph of #y=f(x)=x^3+x+1# is shown in blue, the point #(x,y)=(2,11)# on it is shown, as well as the tangent line with a slope of #13#. The graph of #y=f^{-1}(x)# is shown in green, the point #(x,y)=(11,2)# on it is shown, as well as the tangent line with a slope of #1/13#. These tangent lines have slopes that are reciprocals of each other because of the reflection property across the line #y=x#.


