How can the answer be 106/27? I have worked this problem every way imaginable.
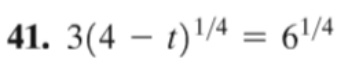
2 Answers
Here's why that is the case.
Explanation:
Your first goal here is to get rid of the exponents, so start by raising both sides of the equation to the fourth power. You need to do that because if you multiply the two fractional exponents by
#[3 * (4 - t)^(1/4)]^4 = (6^(1/4))^4#
This will get you
#3^4 * (4 - t)^((1/4 * 4)) = 6^((1/4 * 4))#
which simplifies to
#3^4 * (4-t) = 6#
At this point, all you have to do is to isolate
#4 - t = 6/3^4#
This is equivalent to
#t - 4 = - 6/3^4#
Add
#t = 4 - (2 * color(red)(cancel(color(black)(3))))/(3^3 * color(red)(cancel(color(black)(3))))#
#t = 4 - 2/27#
You can thus say that
#t = (27 * 4 - 2)/27 = 106/27#
Raise both sides to power of
Explanation:


