How can the distance formula be derived from the pythagorean theorem?
1 Answer
Let's see.
Explanation:
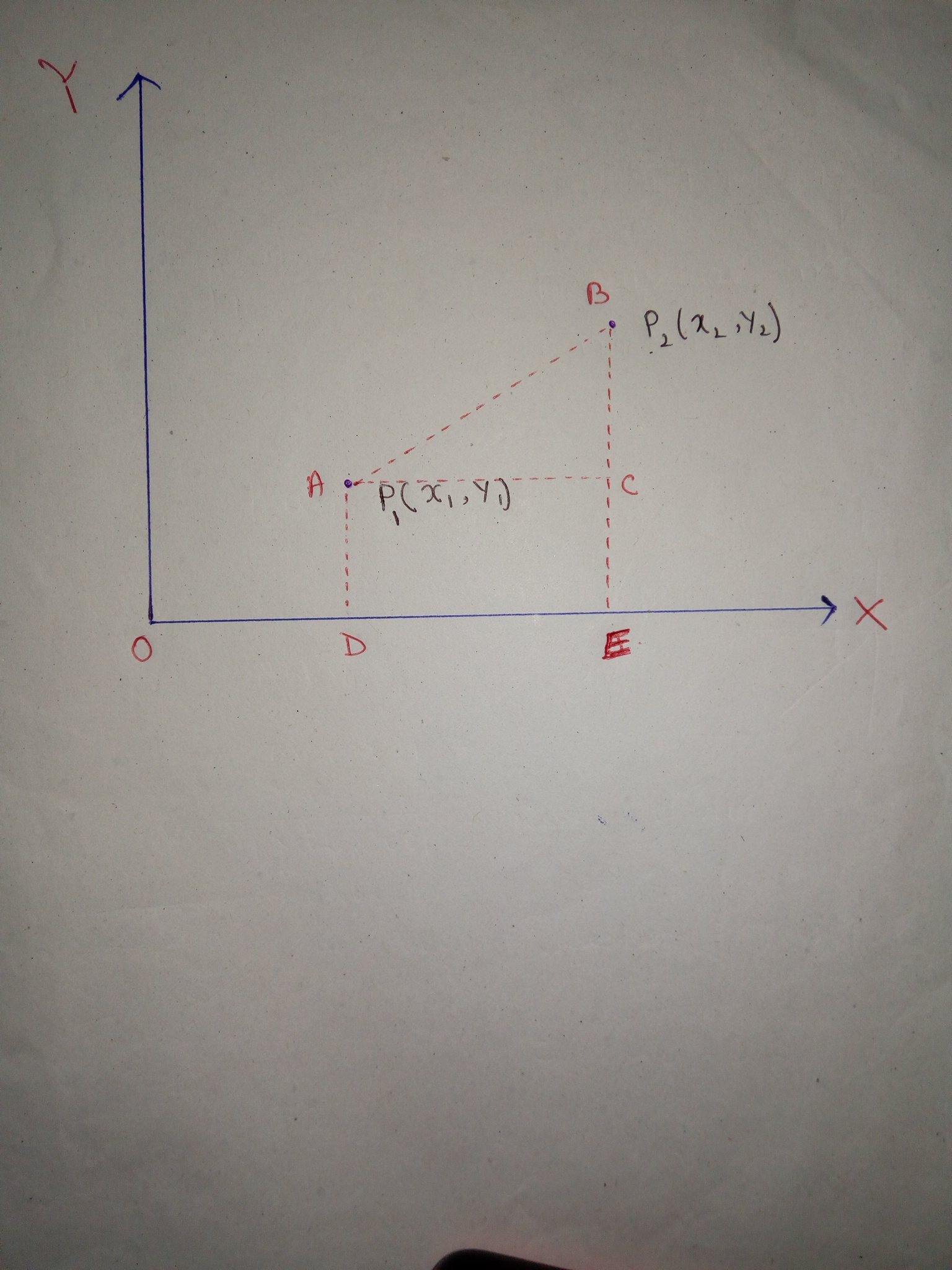
I have drawn a graph in which there are two points
#color(red)(p_1(x_1,y_1))" and "color(red)(p_2(x_2,y_2)# .
- We can easily say that
#" "bar(OD)=x_1" ; "bar(OE)=x_2" ; "bar(AD)=y_1" ; "bar(EB)=y_2# We also have a rectangle
#square OCED# . So,#color(red)(bar(AC)=bar(DE)) " and "color(red)(bar(AD)=bar(CE)# Now,
#bar(AC)=bar(DE)=bar(OE)-bar(OD)=(x_2 -x_1)#
#bar(BC)=bar(BE)-bar(CE)=bar(BE)-bar(AD)=(y_2-y_1)# With the help of Pythagorean theorem,
#bar(AB)^2=bar(BC)^2+bar(AC)^2#
#bar(AB)^2=(x_2-x_1)^2+(y_2-y_1)^2#
#bar(AB)=sqrt((x_2-x_1)^2+(y_2-y_1)^2# N.B:- As it is a square value , you may take
#(x_1-x_2)# or,#(x_2-x_1)# . I mean you have to take difference.That's#(x_1~x_2)#
So, the required formula is proved that
If the distance between two points
#color(green)(p_1(x_1,y_1)# and#color(green)(p_2(x_2,y_2)# is#color(red)(r# ,then,
#color(red)(ul(bar(|color(green)(r=sqrt((x_1-x_2)^2+(y_1-y_2)^2))|# Hope it helps...
Thank you...

