How do I change #int_0^1int_0^sqrt(1-x^2)int_sqrt(x^2+y^2)^sqrt(2-x^2-y^2)xydzdydx# to cylindrical or spherical coordinates?
3 Answers
Hello,
Answer :
I think you don't need to change coordinates. Fubini's theorem says that your integral is
-
Inner integral is
#int_(sqrt(x^2+y^2))^(sqrt(2-x^2-y^2)) dz = sqrt(2-x^2-y^2)-sqrt(x^2+y^2)# . -
Now, you have to calculate
#int_0^(sqrt(1-x^2)) y(sqrt(2-x^2-y^2)-sqrt(x^2+y^2)) dy#
# = -1/2 int_0^(sqrt(1-x^2)) (-2)y sqrt(2-x^2-y^2)dy - 1/2 int_0^(sqrt(1-x^2)) 2y sqrt(x^2+y^2) dy #
#= -1/2 [(2-x^2-y^2)^(3/2)/(3/2)]_0^(sqrt(1-x^2)) - 1/2 [(x^2+y^2)^(3/2)/(3/2)]_0^(sqrt(1-x^2))#
#= -1/3 (1 - (2-x^2)^(3/2)) - 1/3 (1 - x^3)#
#= -2/3 + 1/3 (2-x^2)^(3/2) + 1/3 x^3# -
Finally you have to calculate
#int_0^1 x(-2/3 + 1/3 (2-x^2)^(3/2) + 1/3 x^3) dx#
#= [- x^2/3 - 1/6 (2-x^2)^(5/2)/(5/2) + x^5/15]_0^1 #
#= (-1/3 - 1/15+ 1/15) - (-1/15 2^(5/2))#
# = 1/15 2^(5/2) - 1/3 approx 0.0438#
I haven't finished, but this will get you started.
(Note: there are hemispheres and semicircles in this problem, so there mat be a simple geometric solution. I haven't found one.)
#int_0^1int_0^sqrt(1-x^2)int_sqrt(x^2+y^2)^sqrt(2-x^2-y^2)xydzdydx#
Step 1:
#int_sqrt(x^2+y^2)^sqrt(2-x^2-y^2)xydz=xyz]_(z=sqrt(x^2+y^2))^(z=sqrt(2-x^2-y^2))#
#=xysqrt(2-x^2-y^2)-xysqrt(x^2+y^2)#
Step 2:
#int_0^sqrt(1-x^2)[xysqrt(2-x^2-y^2)-xysqrt(x^2+y^2)]dy#
(to be continued?)
I think this problem wants to be changed to cylindrical or spherical coordinates (But I don't remember how to do that.)
I'm going to ask.
Explanation:
I happened to come across this question and I see that in consideration to what was specifically being asked, it remains unanswered.
Considering the solid that is represented by these integrals (cone and sphere), spherical coordinates are a great choice. This is a lengthly answer, as a lot of students struggle with spherical coordinates and I'd like this explanation to be as helpful as possible.
A good (possibly mandatory) place to start is to get a rough sketch of the solid represented by the integrals. From the limits of integration, we have:
#sqrt(x^2+y^2) <= z <= sqrt(2-x^2-y^2)#
#0 <= y <= sqrt(1-x^2)#
#0 <= x <= 1#
Examining the
#z=sqrt(x^2+y^2)# and#z=sqrt(2-x^2-y^2)# We can look at each equation separately. The first represents a cone. We can see this better by manipulating the equation. Squaring both sides, we get:
#z^2=x^2+y^2# If we set
#x=0# , we get#z^2=y^2=>z=y# . This is a line through the#yz# -plane at#45^o# . Similarly, if we set#y=0# , we get the same line through the#xz# -plane. If#z# is a constant (#>=0# ), we have a circle in the#xy# -plane with radius#z# .The second equation represents a sphere with radius
#sqrt2# . We can see this more easily by squaring both sides and rearranging:
#z^2=2-x^2-y^2=>x^2+y^2+z^2=2# Setting any one variable to
#0# yields a circle with radius#sqrt2# in the corresponding plane of the remaining non-zero variables.As
#z# runs from the cone to the sphere, we are looking at the volume inside both the sphere and the cone. This is a common solid that shows up in problems concerning triple integrals in spherical coordinates.Because spherical coordinates are of the form (
#rho, theta, phi# ), where#rho# represents a sphere of some radius,#phi# represents a half-cone, and#theta# represents a plane, a solid consisting of both a cone and a sphere makes a great candidate for spherical coordinates. In my opinion, it is also easier to evaluate the given triple integral using this coordinate system, so long as you convert the limits of integration and integrand correctly.
Examining the
#y=0# and#y=sqrt(1-x^2)# The first statement tells us that
#y>=0# , meaning that we will start from the origin and concern ourselves only with the part of the solid that pertains to positive#y# values. Or, if you're looking at the axes oriented with the positive#x# axis coming out toward you, we're only concerned with the right side of the solid.The second equation is that of a circle with radius
#1# . We can square both sides and rearrange to see this more easily:
#y^2=1-x^2=>x^2+y^2=1# This tells us that if we push the solid down so that it lies only in the
#xy# -plane, we have a circle with radius#1# , and again, we are only concerned with the right half of the circle.
Examining the
#x=0# and#x=1# The first statement tells us that
#x>=0# , meaning that we will start from the origin and concern ourselves only with the part of the solid that pertains to positive#x# values. Given that we also want only positive#y# values, we know that we only want the part of the solid which lies in the first octant.The second statement reminds us that we are considering the entire radius of the circle, form the origin to the "edge."
Putting all of this information together, the solid represented by the triple integral is contained within a cone and sphere in the first octant. For the purposes of visualization, this is essentially one-fourth of a snow cone.
Here is a graph I've generated with Mathematica:

A view from the top:

Now, the task of rewriting the triple integral in spherical coordinates...
We're given the triple integral in rectangular coordinates, which are likely most familiar to us. This allowed us to get a graph of the solid which we can now use to rewrite in spherical coordinates. Recall that spherical coordinates are of the form (
The variable
#rho# represents the distance we come out from the origin to a point on the edge of our solid. For example,#rho=2# represents a sphere with radius#2# . Our range for#rho# is from the origin to the radus of the sphere,#sqrt2# . Therefore,#rho# runs from#0# to#sqrt(2)# .Next,
#theta# . When we determine the bounds for#theta# , we're looking at the angle from the positive#x# -axis. You can imagine the unit circle is imposed on the#xy# -plane, where the positive#x# -axis begins at#0# . Note that#0 <= theta <=2pi# . It's as though we're taking the positive#x# -axis and revolving it around the origin until we've come back to where we started, forming a circle. In this case, our solid is contained within the first octant, so#theta# runs from#0# to#pi/2# . It is one-fourth of the circle.
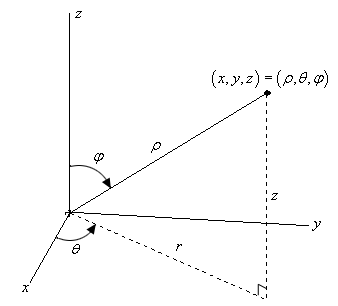
#phi# is also an angle, but illustrates that we are now working in three dimensions. It is the angle beginning from the positive#z# -axis and ending at the negative#z# -axis. In other words,#0 <= phi <=pi# . You can imagine the positive#z# -axis being folded down to overlap the negative#z# -axis to visualize the angle#phi# . Because our solid is contained in the first octant and lies above the#xy# -plane, were are restricted between#phi=0# and#phi=pi/2# . However, because our solid lies within the cone, which has equation#z^2=x^2+y^2# , the furthest#phi# gets is to the edge of the cone at#pi/4# . Recall that#z=y# is the edge of the cone in the#yz# -plane which separates the plane at an angle of#45^o# above the horizontal. Thus,#phi# runs from#0# to#pi/4# . You can also find the point of intersection between the sphere and cone. Plug the equation of the cone into the sphere and solve for#z# . We will use the positive value as we know we are in the first octant where#z# is positive. We put this value along with the value we determined for#rho# into the conversion for#z# to find where the sphere and cone intersect:
#x^2+y^2+z^2=2#
#(sqrt(x^2+y^2))^2+z^2=2#
#z^2+z^2=2#
#2z^2=2#
#z^2=1#
#z=+-1=>z=1# The conversion for
#z# is#z=rhocos(phi)#
#=>rhocos(phi)=1#
#cos(phi)=1/rho# As we know that
#rho=sqrt2# :
#=>cos(phi)=1/sqrt(2)#
#phi=cos^-1(1/(sqrt2))#
#phi=pi/4#
This would be the whole solid, if

We now have our new limits of integration:
#int_0^(pi/4)int_0^(pi/2)int_0^sqrt(2)# Note that
#theta# and#rho# can be flipped, but you will typically see the integration with respect to#rho# first.
Lastly, we need to convert the integrand from rectangular to spherical. Conversions are given as:
#x=rhosin(phi)cos(theta)#
#y=rhosin(phi)sin(theta)#
#dzdydx=>rho^2sin(phi)drhod(theta)dphi#
Putting it all together, we have:
#int_0^(pi/4)int_0^(pi/2)int_0^sqrt(2)(rhosin(phi)cos(theta)*rhosin(phi)sin(theta)*rho^2sin(phi))drhod(theta)dphi#
Which simplifies to:
#int_0^(pi/4)int_0^(pi/2)int_0^sqrt(2)[rho^4sin^3(phi)sin(theta)cos(theta)]drhod(theta)dphi#
We can evaluate the integral as well:
To integrate with respect to
#u=sin(theta)=>du=cos(theta)d(theta)# Note the limits of integration change (
#sin(0)=0, sin(pi/2)=1# ).
#=>(4sqrt2)/5int_0^(pi/4)int_0^(1)[sin^3(phi)u]dudphi#
#=>(4sqrt2)/5int_0^(pi/4)[1/2u^2sin^3(phi)]|_0^1dphi#
#=>(4sqrt2)/10int_0^(pi/4)[sin^3(phi)]dphi#
To integrate with respect to
#=>(4sqrt2)/10int_0^(pi/4)[sin(phi)*sin^2(phi)]dphi#
#=>(4sqrt2)/10int_0^(pi/4)[sin(phi)*(1-cos^2(phi))]dphi#
Now we use a substitution:
#u=cos(phi)=>du=-sin(phi)dphi# Note that the limits of integration change (
#cos(0)=1, cos(pi/4)=(sqrt2)/2# )
#=>-(4sqrt2)/10int_1^(sqrt2/2)(1-u^2)du#
#=>-(4sqrt2)/10(u-1/3u^3)|_1^((sqrt2)/2)#
#=>-(4sqrt2)/10[((sqrt2)/2-1/3(sqrt2/2)^3)-(1-1/3(1)^3)]#
#=>-(4sqrt2)/10(sqrt2/2-sqrt2/12-1+1/3)#
#=>-(4sqrt2)/10((5sqrt2)/12-2/3)#
#=>(4sqrt2)/15-1/3#




