Question

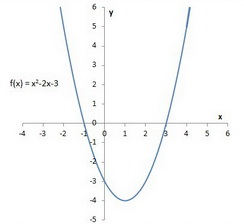
How do I convert the equation `f(x)=x^2-2x-3` to vertex form?

Answer 1

`color(red)( f(x) = (x-1)^2-4)`

The vertex form of a quadratic is given by `y = a(x – h)^2 + k`, where (`h, k`) is the vertex.

The "`a`" in the vertex form is the same "`a`" as in `y = ax^2 + bx + c`.

Your equation is

`f(x) = x^2-2x-3`

We convert to the "vertex form" by completing the square.

Step 1. Move the constant to the other side.

`f(x)+3 = x^2-2x`

Step 2. Square the coefficient of `x` and divide by 4.

`(-2)^2/4 = 1`

Step 3. Add this value to each side

`f(x)+3+1 = x^2-2x+1`

Step 4. Express the right hand side as a square.

`f(x)+4 = (x-1)^2`

Step 5. Isolate `f(x)`.

`f(x) = (x-1)^2-4`

The equation is now in vertex form.

`y = a(x – h)^2 + k`, where (`h, k`) is the vertex.

`h = 1` and `k = -4`, so the vertex is at (`1,-4`).