How do I evaluate #int_0^oo e^-x/sqrtxdx#?
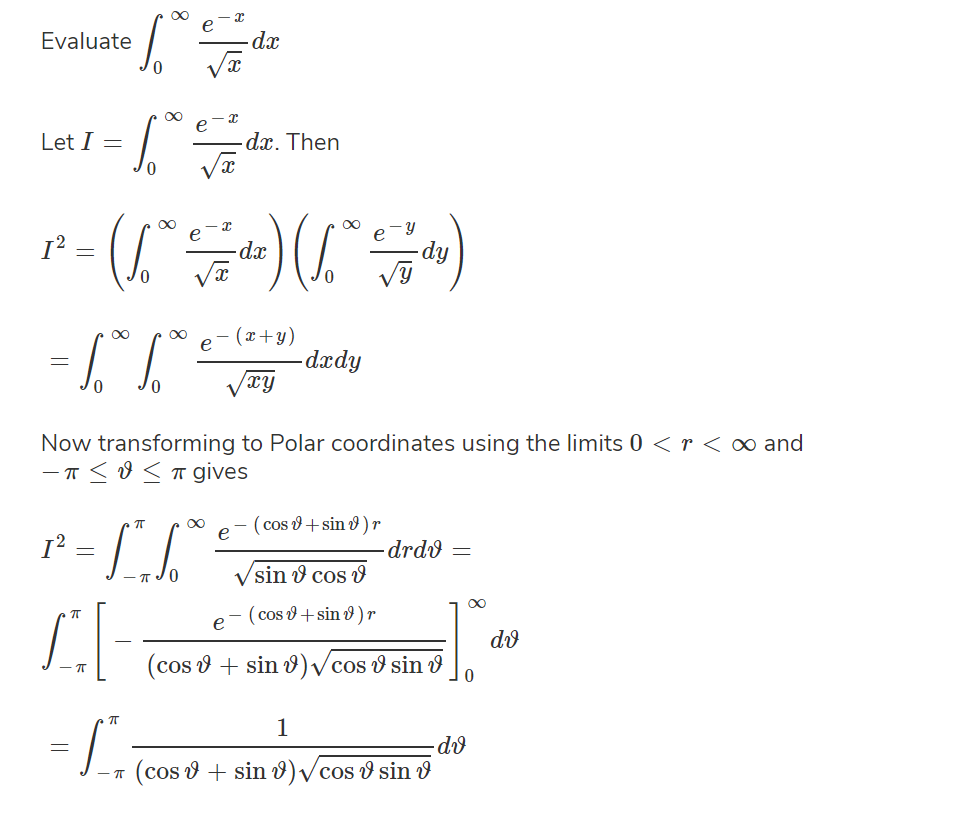
I've gotten this far, but I obviously messed up somewhere because I can't evaluate the second integral.
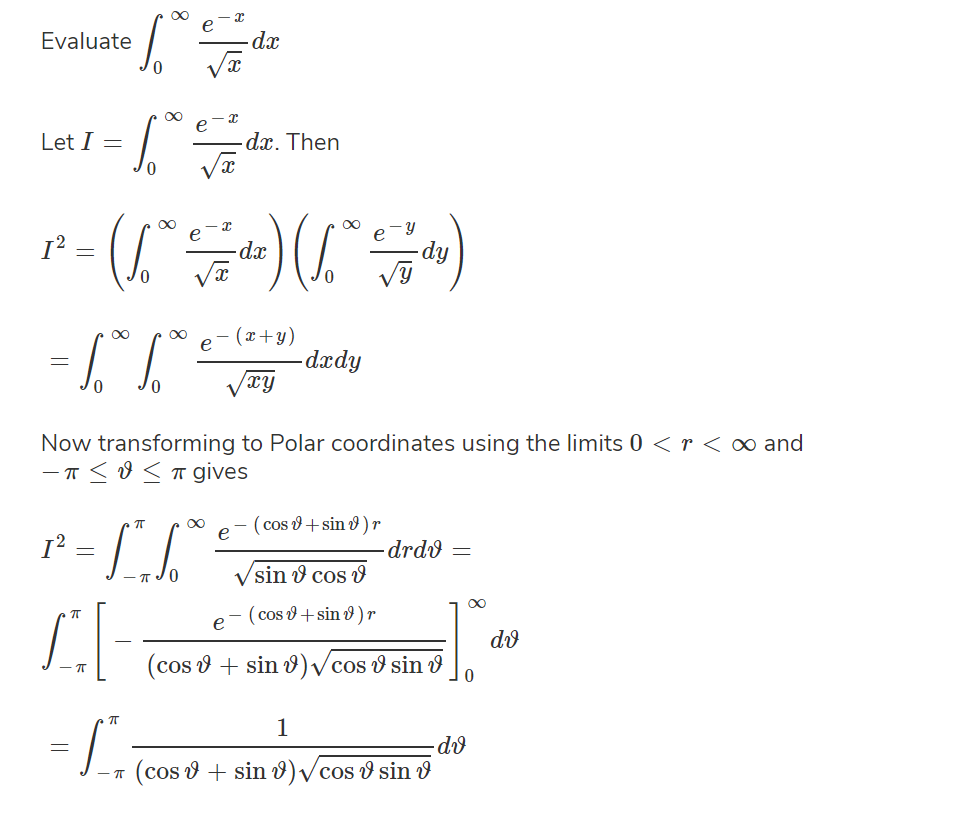
I've gotten this far, but I obviously messed up somewhere because I can't evaluate the second integral.
1 Answer
Mar 28, 2018
# int_0^oo \ e^(-x)/sqrt(x) \ dx = sqrt(pi) #
Explanation:
We seek:
# I = int_0^oo \ e^(-x)/sqrt(x) \ dx #
We can perform a substitution. Let:
# u = sqrt(x) <=> x = u^2 => dx/(du) = 2u#
So that if we substitute into the integral, and change the limits accordingly, we get:
# I = int_0^oo \ e^(-u^2)/u \ 2u \ du #
# \ \ = 2 \ int_0^oo \ e^(-u^2) \ du #
This is related to well studied Gaussian integral, with well known result:
# int_(-oo)^oo \ e^(-u^2) \ du = sqrt(pi) => int_(0)^oo \ e^(-u^2) \ du = sqrt(pi)/2#
Thus, we have:
# I = 2 * sqrt(pi)/2#
Hence:
# int_0^oo \ e^(-x)/sqrt(x) \ dx = sqrt(pi) #

