How do I evaluate sin(pi/3) without using a calculator?

Question

118406 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2015-08-29T16:55:23

#sin(pi/3) = sqrt(3)/2#

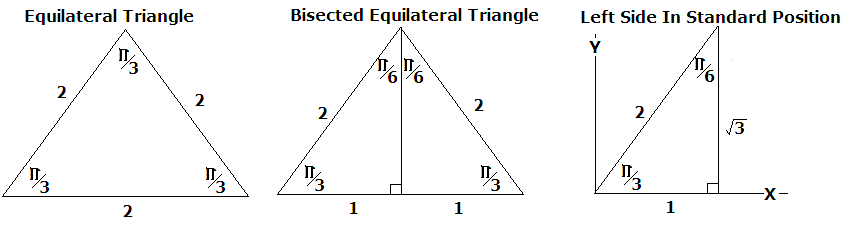
Consider the series of diagrams below.

The interior angles of a triangle always add up to #pi# radians

An equilateral triangle will have all three angles #= pi/3# and all three sides of equal length.

If we set the sides of the equilateral triangle to #2# we can avoid fractions when we divide the triangle into 2 halves vertically,

By the Pythagorean Theorem, the height (the side opposite the angle of #pi/3#) will have a length of #sqrt(3)#

#sin(pi/3) = ("side opposite "pi/3)/("hypotenuse")=sqrt3/2#

enter image source here