How do I evaluate #tan(pi/3)# without using a calculator?

1 Answer
George C.
Apr 8, 2018

Look at a #1#, #sqrt(3)#, #2# right angled triangle to find:

#tan(pi/3) = sqrt(3)#

Explanation:

Note that #pi/3# is the internal angle of an equilateral triangle.

If we bisect an equilateral triangle with side length #2#, then we get two right angled triangles, each with sides #1#, #sqrt(3)# and #2#.

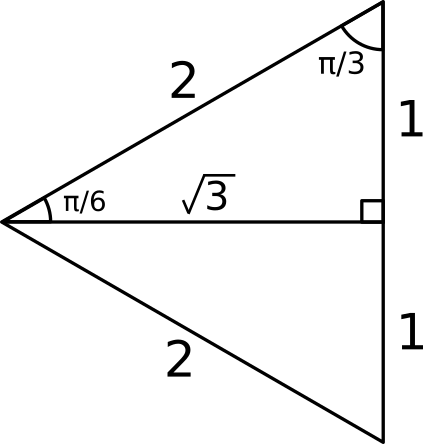
enter image source here

Hence we find that:

#tan(pi/3) = "opposite"/"adjacent" = sqrt(3)/1 = sqrt(3)#

Related questions
See all questions in Trigonometric Functions of Any Angle
Impact of this question
40977 views around the world
You can reuse this answer
Creative Commons License