How do I find a logistic function from its graph?
1 Answer
Hi there. A logistic graph is like an exponential with an upper limit, so it has two horizontal asymptotes, usually y=0 and y=B, as in the "spread of infection" graph here:
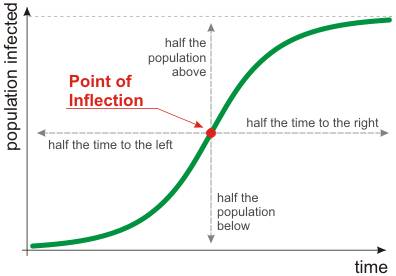
The curve is the solution to the diff eqn
If you have the graph, you can read off the
The next part is to solve for
or the second derivative of the equation for y, and solve!
That part I'll leave for you. You're welcome, from \dansmath/ ;-}
[[Added comment from dansmath: I think the prevailing notation is

