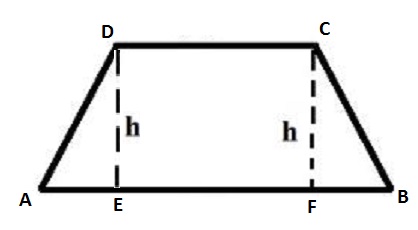
#color(white)(xx)|EF|=|DC|#
#color(white)(xxxxx)=10color(white)(x)"in"#
#color(white)(xx)|AD|=|BC|color(white)(xxxxxxxxxxx)#(isosceles trapezoid),
#color(white)(xx)|DE|=|CF|color(white)(xxxxxxxxxxx)#(isosceles trapezoid),
#color(white)(xx)m(/_ADE)=m(/_BCF)color(white)(xxx)#(isosceles trapezoid),
#color(red)"SAS Postulate"#: Two sides in a triangle have the same length as two sides in the other triangle, and the included angles have the same measure. Therefore
#color(white)(xx)DeltaADE#
and
#color(white)(xx)DeltaBCF#
are congruent:
#color(white)(xx)DeltaADE=DeltaBCF#
#color(white)(xx)|AB|=18color(white)(x)"in""color(white)(xxxxxxxxxxxxxxxxxxxxxx)#(base length)
#=>|AE|+|EF|+|FB|=18color(white)(x)"in"color(white)(xxxxxxxxxxx)#(base length)
#=>|AE|+|EF|+color(red)|AE|=18color(white)(x)"in"color(white)(xxxxxxxxxx)#(SAS Postulate)
#=>|AE|+10+|AE|=18#
#=>|AE|+10+|AE|color(red)(-10)=18color(red)(-10)#
#=>color(red)(1/2xx)2xx|AE|=color(red)(1/2xx)8#
#=>|AE|=4#
#color(white)(xx)cosm(/_DAE)=8/4#
#color(white)(xxxxxxxxxxx)=1/2#
#=>cosm(/_DAE)=cos60#
#=>arccoscosm(/_DAE)=arccoscos60#
#=>m(/_DAE)=60#

