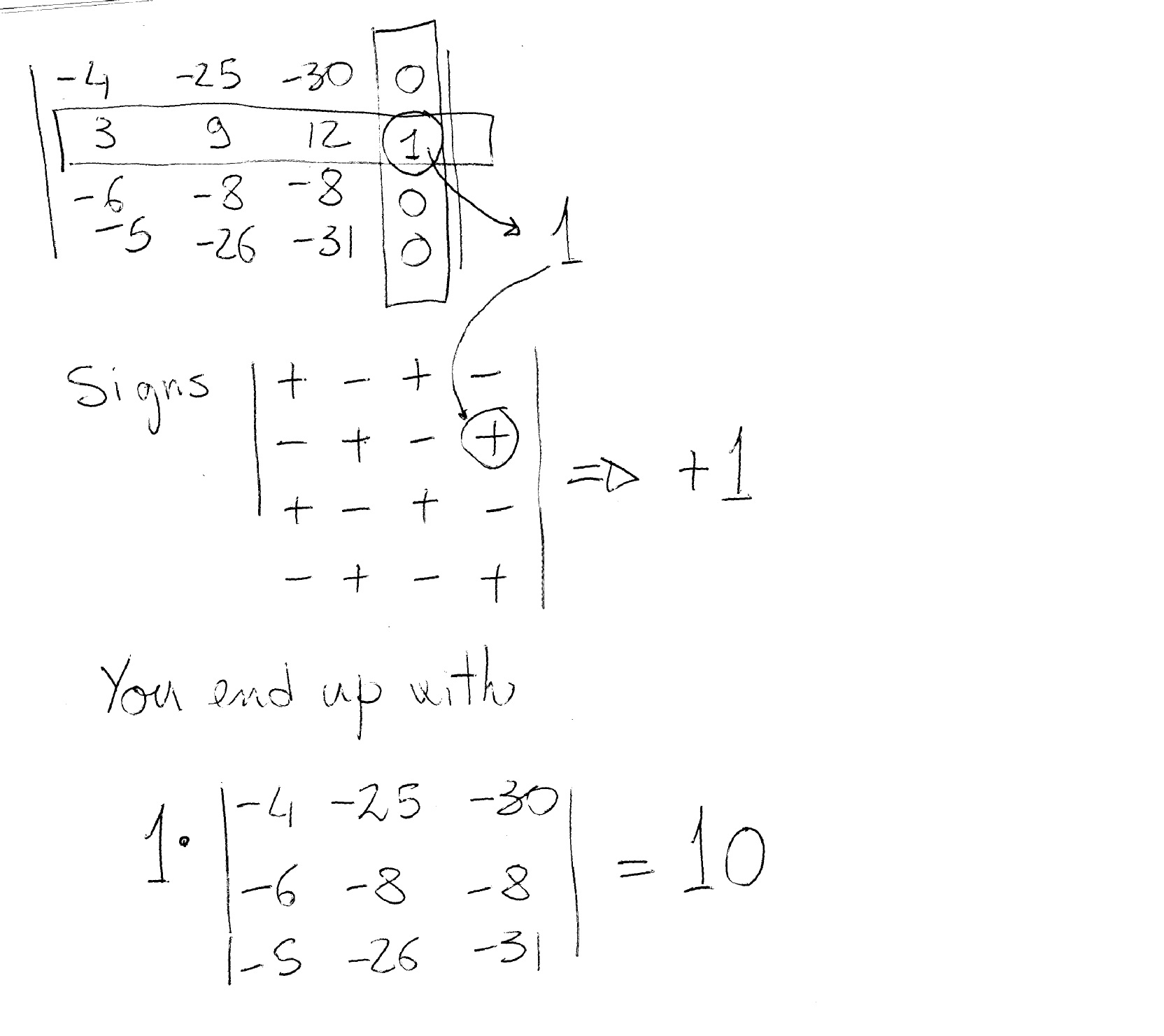How do I find the determinant of of a #4xx4# matrix?
2 Answers
Recursively in terms of determinants of
Explanation:
Given a matrix:
Duplicate the first three columns to form three extra columns. Then for each of the first
I have two main methods:
Explanation:
You have two main ways to find the determinant of a matrix
1] Using the method of Laplace or of the Cofactors. This method is good and easy to apply but very cumbersome! You must evaluate a lot of smaller determinants and it is possible, during these steps, to make mistakes (it also quite boring!!!):
For example:
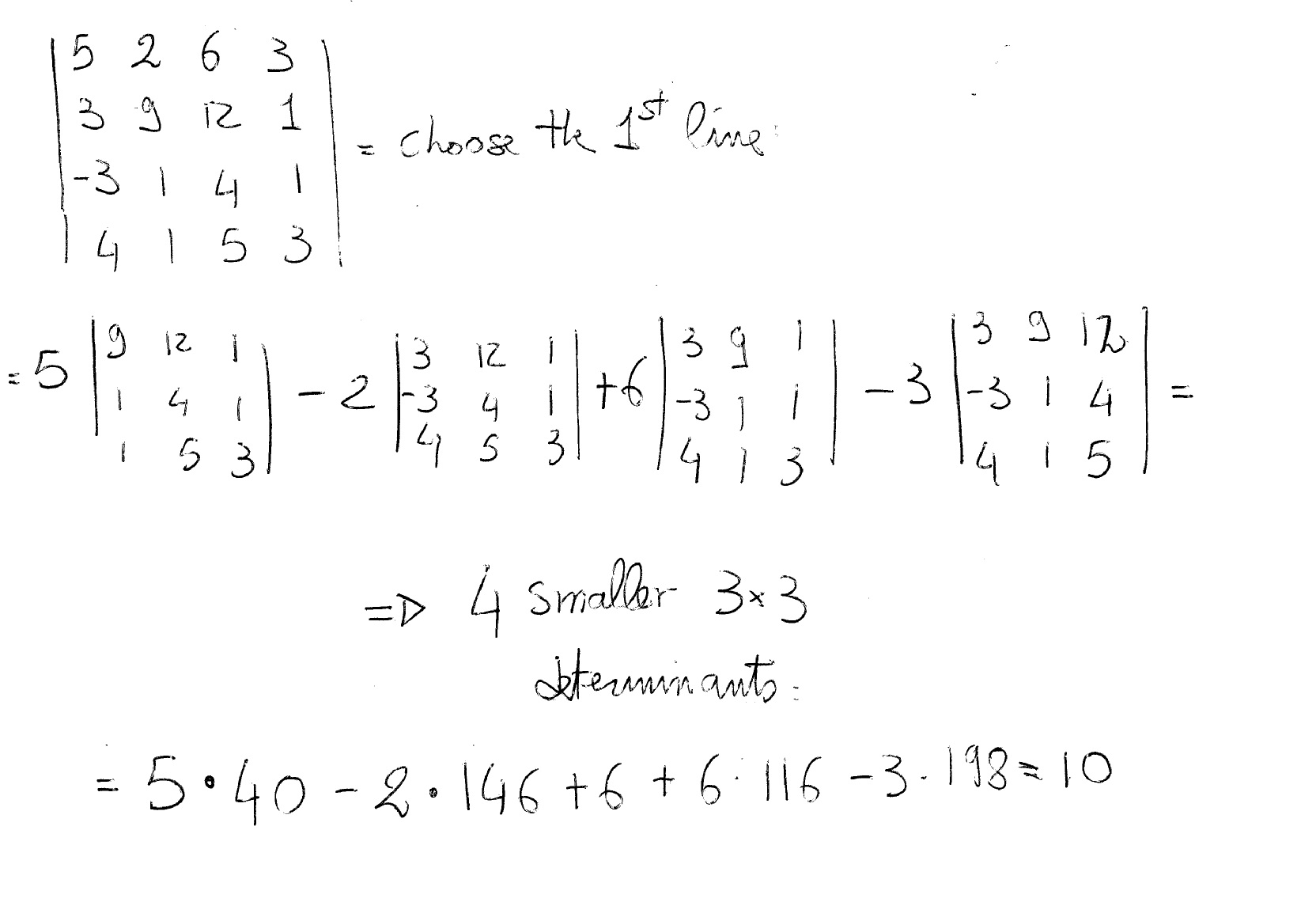
2] The second way is a little bit more fun but a little bit more daring. You must (through operations on lines or columns) get a line or column of all zeroes but one.
The operations you are allowed to make are:
- add or subtract 2 lines or columns;
- multiply the elements of one line or columns times a number and then add or subtract to another line or column. For example:

Extract the number at the crossing (with the right sign) and use it together with the remaining